そこにデータムを付けるのか、付けないのか:製図を極める! 幾何公差徹底攻略(6)(1/2 ページ)
今回は製図の際に多くの設計者が戸惑う悩みの1つ「データムを付けるのか付けないのか」をスッキリ解決する。
前回、幾何公差の種類と公差領域を学習しました。今回は4つの幾何特性(形状公差・姿勢公差・位置公差・振れ公差)のうち基本となる形状公差を学習します。形状公差の中には、その名称から比較的理解しやすい特性から意外と多くの技術者が勘違いして理解したり苦手意識を持ったりしているものまでさまざまなものがあります。まずは形状公差をしっかりと理解しましょう。
形状公差とは
「形状公差」とは、対象となる形体(平面や線など)が、幾何学的に正しい形状(Form)を表す偏差の許容値内にあるかを規定することです。幾何公差の分類の中で、唯一単独形体と呼ばれ、データムを必要としないことが特徴です。
形状公差を簡潔に説明すると、「まっ平ら(たいら)」「まん丸」といった絶対形状や図面に指定された形状とを比較する特性であることです。つまり姿勢公差・位置公差・振れ公差がデータムという相対比較する基準を持つのに対して、形状公差は相対比較するデータムを持たずに絶対形状と比較する特性であることを、まず認識してください。形状公差を指示する場合はデータムが必要ないのです!
上記を理解できれば、製図の際に多くの設計者が戸惑う悩みの1つ「データムを付けるのか付けないのか」が解決されます。
形状公差には、次の6つの幾何公差があります。
- 真直度(Straightness)
- 真円度(Roundness)
- 線の輪郭度(Profile of a line)
- 平面度(Flatness)
- 円筒度(Cylindricity)
- 面の輪郭度(Profile of a surface)
このように6種類もある形状公差は、「2次元領域」か「3次元領域」の2つのグループに分類できます(図1)。
形状公差として6種類の原理を覚える必要はなく、2種類の原理を理解すればあとはそれを応用したものといえます。
幾何公差は難しいと敬遠してきた皆さんも、少し気が楽になったのではないでしょうか。
“線で評価する”“面で評価する”といわれて、皆さんはどのように想像するでしょうか? “面で評価する”といわれた場合、比較的イメージが付きやすいと思います。例えば、面を想像すると、身近なものでは「テーブルの上面」「円筒面」「高級スポーツカーのボディ曲面」などさまざまな面を想像できます。
しかしこれらはリアルな世界の実在する面を表し、実在する面以外に仮想の面を想像できなければいけません。仮想の面とはどのようなものでしょうか?
医療の分野でよく耳にする「CT」(コンピュータ断層撮影)は、コンピュータを使って物体の内部を断面に輪切りにして画像を得る技術のことです。それから得られた切り口の画像が仮想の面なのです。
次に、“線で評価する”といわれた場合、線を想像すると「円筒の中心軸線」以外になかなか思い付くものがありません。そう線は意外と想像できないものです。実は“線で評価する”とは、糸やナイフエッジのような線が存在するものを探していては見つけることができません。幾何特性における線は、図面を読む人が自ら線を作り出さないといけないのです。
どうやって線を作るかというと、子供のころ、誕生日に家族で食べたホールケーキを想像してみてください。ホールケーキは一般的に円筒形状のため線という意識が余りありません。ホールケーキを食べる場合、そのまま食べる人はまずいないと思います。どうするかというとショートケーキの形状に切り取り小分けして食べます。
このときケーキの切り口には切断面ができ、その稜線は線という成分で構成されます。
このように、形状公差にかかわらず幾何公差を考えるときは、リアルに見える面以外に、想像力を働かせて切り口として見える切断面や、その切断面の稜線を想像できなければ解釈ができないのです!
幾何公差の作法を駆使することでさまざまな解釈を表現することができます。本連載では、6つの形状公差の定義とともに、よく使われるであろう代表図面指示例をあわせて確認していきます。
真直度
JISによると、「真直度(Straightness)とは、直線形体の幾何学的に正しい直線からの狂いの大きさをいう」と定義されます。真っすぐであって欲しいという形体に対して指示するものです。
特に細長い軸や角柱などでは、加工熱によって反りが発生する可能性が高くなります。機能上、反りが許されない場合に用います。
図2に示す図面例は、丸軸の中心軸線が直径0.1mmの曲がりのない円柱の中にあれば合格品と判断されるものです。丸軸における中心軸線が対象部位ですので、全方位を意味する直径範囲で幾何公差値を指示した例です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
 図1 形状公差の分類
図1 形状公差の分類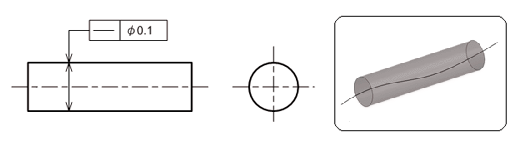 図2 丸軸の中心軸線
図2 丸軸の中心軸線





