幾何特性の領域把握がはじめの一歩だ!:製図を極める! 幾何公差徹底攻略(5)(1/2 ページ)
まず幾何特性が定義できる領域から理解しよう。4つの幾何特性分類、図面指示する上での注意点なども解説する。
前回、幾何公差の基礎となるデータムを学習しました。今回は、幾何特性の全体像を把握するために、まずは幾何特性が定義できる領域から理解します。さらに幾何公差は4つの幾何特性で分類されること、図面指示する上での注意点を学習します。
幾何公差の基本概念
JISには、次のように幾何公差の基本概念が定義されています。これらの定義の中でポイントとなる部分に下線を引き、補足解説を示します。
1.「形体に指示した幾何公差は、その中に形体が含まれる公差域を定義する」
幾何公差が示す領域は公差値で示された数値の幅を表し、その領域の中に該当する形体が収まるか収まらないかを判断するものです。
2.「形体とは、表面、穴、溝、ねじ山、面取り部分または輪郭のような加工物の特定の特性の部分であり、これらの形体は、現実に存在しているもの(例えば、円筒の外側表面)または派生したもの(例えば、軸線または中心平面)である」
公差形体は現実に存在する表面や線など(母線という)と、それらから現実に定義できるもの(中心軸線や中心平面など)の2種類に分かれます。
3.「公差が指示された公差特性と寸法の指示方法によって、公差域は次の1つになる」
公差領域は、必ず下記に示す7つの領域となります。
4.「さらに限定した公差が要求される場合、例えば注記を除いて、公差付き形体はこの公差領域内で任意の形状または姿勢でも良い」
公差形体は、上記に示す領域の中にあれば、どのように変形していても問題ありません。
5.「特に指示した場合を除いて、公差は対象とする形体の全域に適用する」
特別な記号を用いずに表した幾何公差の対象範囲は、矢を当てた面や線が稜線など変化点のある部分までの領域全体を指します。
6.「データムに関連した形体に指示した幾何公差は、データム形体自身の形状偏差を規制しない。データム形体に対して形状公差を指示しても良い」
データム指示した面や線は、特に幾何特性の規制を受けません。一般的に暗黙の了解としてのデータムなので、それなりの幾何特性に仕上げると解釈されますが、幾何特性を指示する方が望ましいとされます。
以下の表1に、4つに分類された幾何公差の記号と特性を示します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
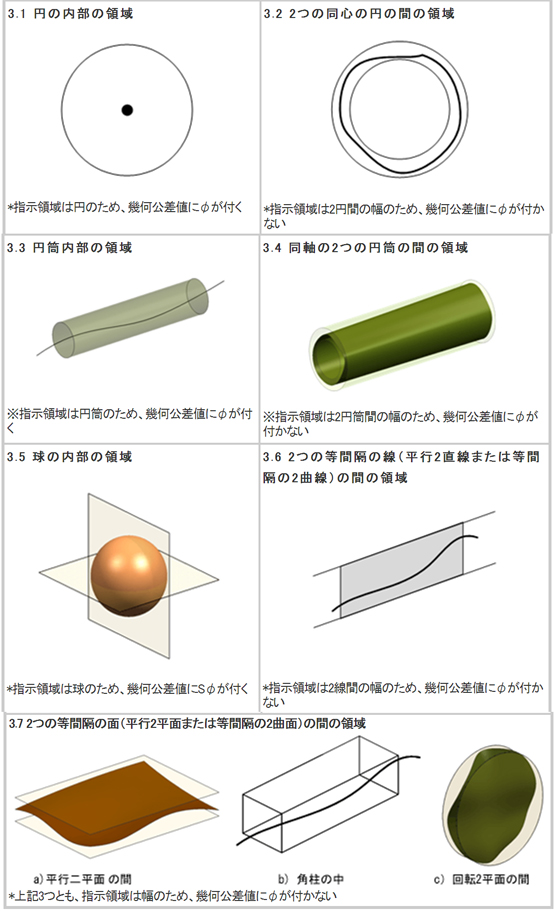
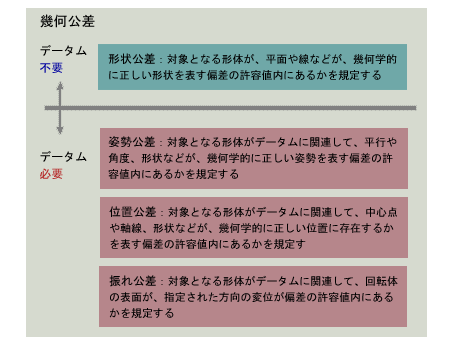 図1 幾何公差の分類
図1 幾何公差の分類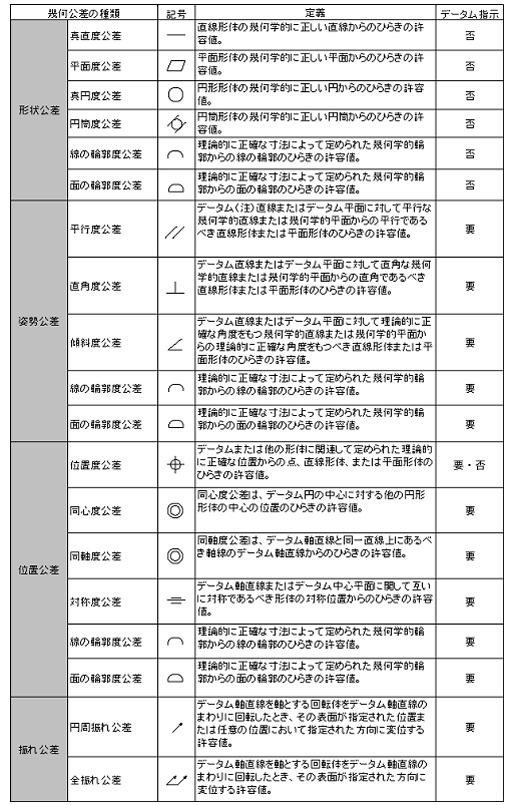 表1 幾何公差記号一覧
表1 幾何公差記号一覧





