車の運転制御を風呂の水位制御に置き換える:独学! 機械設計者のための自動制御入門(5)(4/4 ページ)
積分補償だけではダメ?
喜ぶのはまだ早いで。確かに、目標水位に達すると、偏差hが0となって、モータはあるバルブ開度xで停止する。だけど、その開度が漏れ流量qを補充するのに必要な開度xAであるという保証はどこにあるねん?
だって夢の中では、水位はそれ以上、上がらなかったよ
……ぷっ!
銀二さんは思わず笑ってしまいました。彼は経験上、単純な積分補償だけではうまくいかないことを知っていました。その理由を草太に説明するためにボード線図を書き出しました。
前回、積分要素の周波数応答特性について説明したやろ。ここで復習してみようか。伝達関数をG=y/xとして、入力x=χ・sin(ωt)を時間積分すると、出力は、
y=−χ/ω・cos(ωt)=χ/ω・sin(ωt−π/2)
となる。
G=y/xだから、
|G|=1/ω
∠G=−π/2 (ラジアン)=−90 (°)
となることは理解できるよな
うん。ゲイン(dB)は、20・log|G|=−20・log(ω)だね
いま草太が書いているブロック線図のコントローラG1には、積分に係数bが掛かっているから、ゲイン特性はbの値に応じて20・log(b)上下するわけや。つまり……、
ゲイン(|G1|)=20・{ log(b)−log(ω)} (dB)
位相∠G1=−π/2=−90 ( °)
(8)
そしてバルブ流量特性の伝達関数G2はG2=y/xとしてy=a・xだから、
ゲイン(|G2|)=20・log(a) (dB)
位相∠G2=0 ( °)
(9)
最後に、浴槽の流量−水位特性についての伝達関数もG1と同じく積分だ。ただし浴槽の断面積Sで割っているから、
ゲイン(|G3|)=−20・{log(ω)+log(S)} (dB)
位相∠G3=−π/2=−90 ( °)
(10)
だ
このブロック線図は車の場合と同じ構成だね。すると、開ループシステムの伝達関数Goを(11) として……(12)
(8)(9)(10)から、草太はそれぞれの伝達関数の周波数応答特性のボード線図を描いてみました(図10)。Go=G1・G2・G3のボード線図は、G1、G2、G3の各ボード線図を足し合わせたものとなることは以前説明したとおりです。
Go、G3のゲインはともに低周波域で∞(無限大)だね。GoとG3のゲインの差も同じく低周波域で∞となるから(12)式の右辺第2項は0となって目標水位Hoに到達するんじゃないの?
草太は自分の考えが間違いないことに自信を持ち、前回教えてもらった理論を早速応用しました。もしこれで違うのであれば、銀二さんが教えてくれた理屈自体に誤りがある、とさえ思いました。
草太の説明が成立するためには、その前提として開ループシステムGoが安定であることが必要だぜ。Goは安定かい?
Goが安定かどうかは位相余裕や、ゲイン余裕を調べればよかったよな。 ……うん? ……あれれ? ゲインが0dBのときの、−180度との位相差は0だね。つまり位相余裕は0ってこと? 位相が180度遅れたときのゲイン余裕はどう見ればいいの? ゲイン余裕は存在しない? これはどういうこと?
どうもこうもあらへんがな。位相余裕は0っちゅうことや。開ループシステムの伝達関数Goは全周波数において位相が180度遅れているから、要するにシステムは不安定というこっちゃな。Goの位相曲線は周波数に対して一定で、−180度の位相線と交わる“1つの点”は存在しないから、もはやゲイン余裕など意味があらへん
不安定?
目標水位に達して、偏差hが0となり、モータが、あるバルブ開度で停止しようとするけれど、その開度は漏れ流量qを補充するのに必要な開度xA以上あるっていうことやな。だから、止まってほしいのに、水位Hは目標水位Hoを超えてどんどん上がる。すると偏差hはマイナスとなるから、バルブのモータはバルブを閉めるわな
今度は漏れ流量qで水位が下降して目標水位に達することになるけど、モータは偏差の時間積分量に比例した開度でしか給湯バルブを開こうとしないから、すぐにはxAまで開かない。xAまで開いても、水位はHoより下にあるからバルブモータはバルブをもっと開けようとする。こうして、水位は再び上昇してHoを超える。延々とこの繰り返しが続いて、図11のように浴槽の水位は上がったり下がったりするっていうことやね!
えっと……?
草太は戸惑いました。比例制御では、偏差が存在しない限り漏れ流量qに応じたバルブの開度に設定することができませんし、積分補償では水位を一定に保つことができません。それでは、どうやったら漏れ流量の大きさに関係なく、自動的に目標水位へ到達させ、その状態を維持することができるのでしょうか。
この問題が解決できれば、風による車の斜行の問題も解決できそうです。次回はこれらの問題を解決する中で、安定性改善の代表的な補償方法である、位相進み補償についての学習をします。
筆者より(補足と付録)
(2)〜(7)の浴槽の水位制御の微分方程式を、オイラー法によってエクセルで解いた図11の例を付録として紹介しておきます。この事例によって、積分補償だけでは、浴槽水位を一定に保つことができないことを体感できると思います。
*計算内容のExcelデータ(jido05.xls)のダウンロードはこちらから可能です(Microsoft Excel 2003以上でご覧ください)。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞





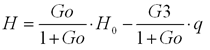
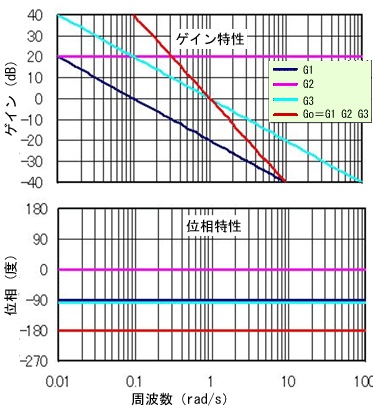 図10 浴槽水位制御のボード線図
図10 浴槽水位制御のボード線図 
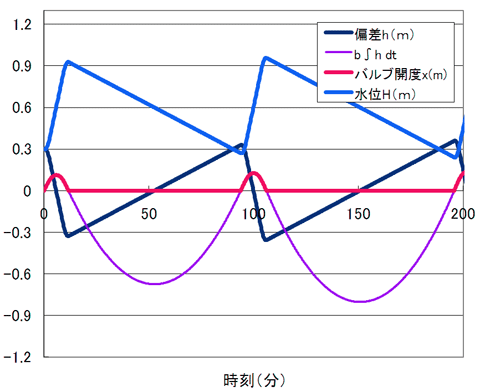 図11 積分補償による浴槽水位制御
図11 積分補償による浴槽水位制御 






