車の運転制御を風呂の水位制御に置き換える:独学! 機械設計者のための自動制御入門(5)(2/4 ページ)
自動車の制御と浴槽の水位制御
銀二さんにいわれて、草太が描いたのが図2です。
車がガードレールに当たりそうだと気付いたときは、大きくハンドルを切るよね。そしてセンターラインに近づけばハンドルを切る角度は小さくする。でも、ハンドルの角度は0にはできないよ。だって、それでは風に押し流されてしまうからね
そうだよな。最初は大きく切って、最後は5度となるようすればいいってことやな。でも、風はいつも車を5度斜行させる強さで吹いているとは限らない
そうだよね。そこが問題なんだよね。人間は風の強弱とは無関係に、車が元の位置に戻り、かつ車が斜行しないハンドル角度に到達すれば、ハンドルを切るのをやめるんだよね
そうや、そうや。それを機械にやらせるにはどうしたらいいかってことや
そういいながら、銀二さんは、今日、技術士仲間との勉強会があるのを思い出しました。
ちょっと用事を思い出した。すまんけど、それまで自分で考えとってくれへん? 2、3時間で帰ってこられると思うわ
そういい残して銀二さんは、書斎からいそいそと出ていきました。
仕方なく、草太は自分で考えることにしました。ボンヤリ窓から外の景色を眺めていると、淡路島の上を白い雲が流れていくのが見えます。聞こえるのはひばりの鳴き声だけ。
……だんだん、草太のまぶたが重〜くなってきました。
昨日の夜、お風呂に浸かりながら眺めた夜景もきれいだったなぁ……ムニャムニャ
――草太は眠ってしまったようです。
そこで、目が覚めました。草太は放心したように、しばらく淡路島の上に浮かぶ白い雲を眺めていました。
うん? まてよ。水漏れによる浴槽の水位低下を横風による車の斜行、お湯の蛇口のバルブの開度を車のハンドル角度とすれば、浴槽の水位を元に戻そうと急いでバルブを開くことと、横風にあおられて横に振られた車の位置を元に戻そうと急いでハンドルを切ることは、同じ操作じゃないのかな?
草太は、車の制御の問題をもっと分かりやすい浴槽の水位制御の問題に置き換えて考えることにしました。そのために、一連の操作を図4のように整理してみました。
まず、給湯流量Q(m3/s)は蛇口のバルブの開度x(m)に比例するから、比例定数をa(m2/t)として、
Q=a・x (2)
とおいて考えてみよう(図5参照)
(図4の)1と2から、補充すべきお湯の流量を目標水位Ho(m)と現在の水位H(m)との偏差h(m)に比例する案も考えられる。しかしそれだと、車の場合とまったく一緒だよな。僕が夢で蛇口のバルブをひねった感じでは、水位が低ければ低いほど、“急いで”蛇口をひねってバルブの開度xを広げたよな。そして、湯船にお湯がいっぱいに近づくにつれて、“ゆっくり”ひねった。“急いで”は、バルブを開く速度が速いことを意味するから、これを数式で表現すれば……
偏差hに比例して、蛇口のバルブを開く速度を変えるんだから、比例係数をb(1/s)とすれば……
さらに、湯船の断面積をS(m2)、漏れ流量をq(m3/s)とすると、水位H(m)は、Qが大きければ大きいほど増加し、漏れqが大きければ大きいほど減少するから……
現在の水位Hが分かれば偏差hが求められるから(4)からそれを積分すればバルブの開度xが分かる。バルブ開度xが分かれば(2)から給湯流量Qが分かり、(5)から、積分して水位Hが分かる。うーん。このフローを分かりやすくするために、ブロック線図に描いて整理してみよう
草太は、浴槽の絵と水位制御のブロック線図(図6および図7)を描いてみました。
なんか車の自動運転のブロック線図とよく似てるな。G3の入力は流量Q−qで出力が水位Hだから、制御対象G3の伝達関数というのは(5)式を積分したものなんだ。 つまり……(6)
ということだな。すると、バルブ開度xについても(3)式から、偏差hを積分したものとなって、伝達関数G1も同じく積分ということか(7)
草太は、目標水位と現在の水位との偏差を積分した値に比例して、蛇口のバルブを開閉すれば、漏れ流量qの大きさに関係なく、“自動的”に目標水位にまで到達するように思えてきました。しかし絶対的な自信はありません。
そこへ、勉強会を終えた銀二さんが帰ってきました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

 図2 人間の運転制御
図2 人間の運転制御 




 図3 浴槽の水位制御
図3 浴槽の水位制御  図4 バルブの手動制御による浴槽の水位制御フロー
図4 バルブの手動制御による浴槽の水位制御フロー 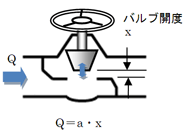 図5 手動バルブ
図5 手動バルブ 

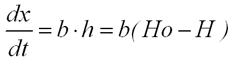

 図6 水漏れがあるときの浴槽水位制御
図6 水漏れがあるときの浴槽水位制御 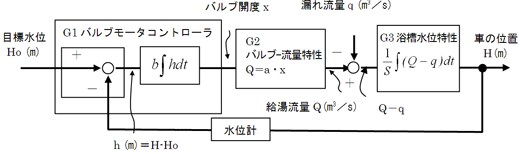 図7 水漏れがあるときの浴槽水位制御
図7 水漏れがあるときの浴槽水位制御 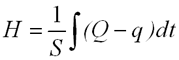 図
図





