音振動のモデリング 〜実際の製品をモデリングする際のさまざまな手法〜:1Dモデリングの勘所(7)(4/4 ページ)
音振動のエネルギー視点でのモデリング
最後に、音振動のエネルギー視点でのモデリングについて説明する。ここでは、考え方と適用例を簡単に述べるのみにとどめるので、詳細は参考文献[2]を確認してほしい。
図8に考え方を示す。対象物を複数の要素に分け、入力となるパワーと各要素のエネルギーの関係を定義する。ある要素にパワーが入力されると、一部は内部損失パワーとして消費され、一部は周辺要素に伝達され、各要素にはエネルギーが蓄積される。パワーの平衡式は電流則に相当し、パワーとエネルギーの関係は電圧測(オームの法則)に相当する。最終的には、
で表現され、知りたい周波数帯ωを決めて、入力パワーPを与え、各要素および要素間の損失率Lを定義することにより、各要素のエネルギーEを算出する。
損失率は、各要素自体の内部損失パワーと各要素間の伝達パワーとで定義方法が異なる。前者の内部損失パワーは、材料減衰の説明で触れた損失係数ηを用いて定義される。一方、後者の各要素間の損失率は、各要素の物性値(縦弾性係数、密度、ポアソン比)、形状(面積、接続長さ、厚さ)から決定される。このように、概略の形状のみで、境界条件などは必要ないため、詳細形状、構造が決まらない構想設計段階でも適用できるというメリットがある。
図8に示したように、この方法では最終的に各要素のエネルギーが算出される。音振動のエネルギーは図9のように定義されるので、この関係式から振動速度および音圧の実効値を知ることができる。
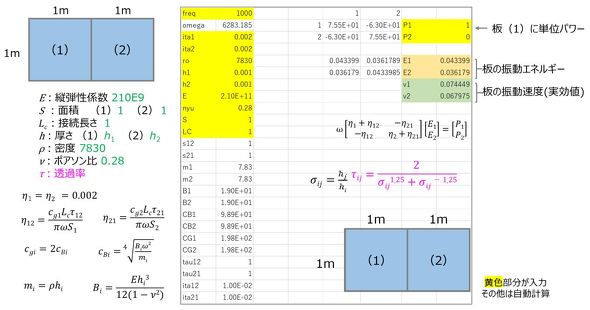
図10に、2つの板から構成される構造物の振動問題への適用例を示す。この方法は、最終的には連立方程式を解くことになるので、表計算ソフトで解析可能である。ここでは、2つ矩形(くけい)板があり、その1辺で接合されている状態を考える。図10中に黄色で示した項目が入力値で、後は自動計算である。対象周波数を1000Hzとし、矩形板(1)に単位パワーを与えた際の各矩形板(1)および(2)の振動エネルギー(振動速度の実効値)の算出例である。図10左下に、損失率の定義式を示す。定義式の理解には若干の時間を要するが、これさえクリアすれば計算自体は単なる算術計算である。
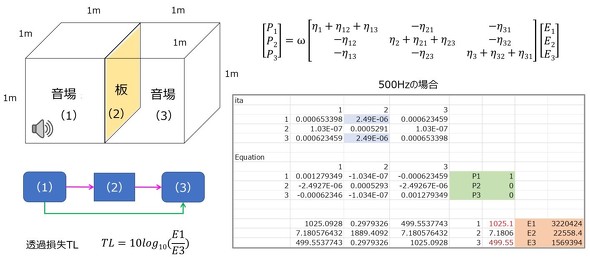
図11に、板で隔てられた2つの音場への適用例を示す(参考文献[3])。対象周波数を500Hzとし、音場(1)に単位音響パワーを入力し、板の振動エネルギーならびに各音場の音響エネルギーを算出している。各音場のエネルギー、E1、E3から等価損失
を予測することも可能である。
参考文献:
- [2]R.Lyon and R.G.DeJong,Theory and Application of Statistical Energy Analysis,2nd Edition,Butterworth-Heinemann,1995
- [3]M.J.Crocker and A.J.Price,Sound Transmission Using Statistical Energy Analysis,J.Sound Vib.(1969)9(3)
次回は、振動のモデリングの具体例として、ランドリー(洗濯機)の振動モデリングについて考える。 (次回へ続く)
筆者プロフィール:
大富浩一(https://1dcae.jp/profile/)
日本機械学会 設計研究会
本研究会では、“ものづくりをもっと良いものへ”を目指して、種々の活動を行っている。1Dモデリングはその活動の一つである。
- 研究会HP:https://1dcae.jp/
- 代表者アドレス:ohtomi@1dcae.jp
関連記事
 1Dモデリングの方法にもさまざまなアプローチがある
1Dモデリングの方法にもさまざまなアプローチがある
「1Dモデリング」に関する連載。連載第4回では、本題である1Dモデリングの方法を取り上げる。まず、1Dモデリングの方法には大きく「モデル生成」「低次元化モデリング」「類推モデリング」の3つのアプローチがあることを説明。特に本稿では1Dモデリング固有の考え方としての類推モデリングについて詳しく解説する。 0Dモデリングとは? 理論・経験に基づく理論式・経験則が究極の1Dモデリング!?
0Dモデリングとは? 理論・経験に基づく理論式・経験則が究極の1Dモデリング!?
「1Dモデリング」に関する連載。連載第3回は、理論・経験に基づく理論式・経験則が究極の1Dモデリングであることを、0Dモデリングの定義、3Dモデリングとの関係、幾つかの事例を通して説明する。また、理論・理論式を考えるに当たって重要な“単位”に関して、なぜ単位が必要なのかその経緯も含めて紹介する。 1Dモデリングとは? モデリングをさまざまな視点から捉えることで考える
1Dモデリングとは? モデリングをさまざまな視点から捉えることで考える
「1Dモデリング」に関する連載。連載第2回は、モデリングをその表現方法から2種類の“3つのモデリング”に分けて考える。次に1Dモデリングが必要となる背景について、1DCAEとMBDという2つの製品開発の考え方を紹介し、これらと1Dモデリングの関係を示す。さらに、リバース1DCAEと1DCAEを通して、より具体的に1Dモデリングのイメージを明らかにする。以上を通して、最後に“1Dモデリングとは”について考察する。 モデリングとは何か? 設計プロセスと製品設計を通して考える
モデリングとは何か? 設計プロセスと製品設計を通して考える
「1Dモデリング」に関する連載。連載第1回は、いきなり1Dモデリングの話に入るのではなく、そもそもモデリングとは何なのか? について考えることから始めたい。ものづくり(設計)のプロセス、製品そのものを構成する要因を分析することにより、モデリングとは何かを明らかにしていく。 なぜ今デライトデザインなのか? ものづくりの歴史も振り返りながら考える
なぜ今デライトデザインなのか? ものづくりの歴史も振り返りながら考える
「デライトデザイン」について解説する連載。第1回では「なぜ今デライトデザインなのか?」について、ものづくりの変遷を通して考え、これに関する問題提起と、その解決策として“価値づくり”なるものを提案する。この価値を生み出す考え方、手法こそがデライトデザインなのである。 デライトデザインとは? 3つのデザイン、類似の考え方を通して読み解く
デライトデザインとは? 3つのデザイン、類似の考え方を通して読み解く
「デライトデザイン」について解説する連載。第2回では、デライトデザインとは? について考える。まず、設計とデザインの違いについて触れ、ユーザーが製品に期待する3つの品質に基づくデザインの関係性にも言及する。さらにデライトデザインを実行する際に参考となる考え方や手法を紹介するとともに、DfXについて説明し、デライトデザインの実践に欠かせない要件を明確にする。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
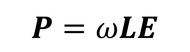 式11
式11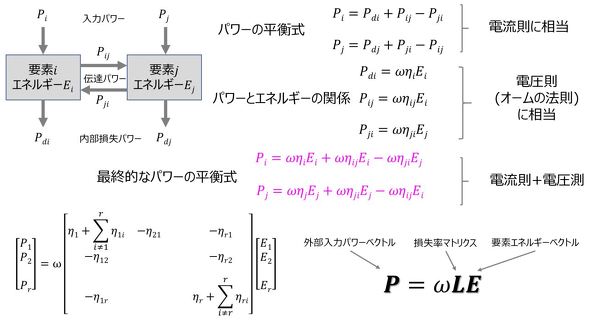
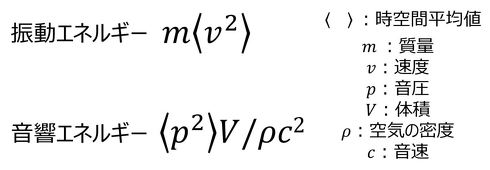
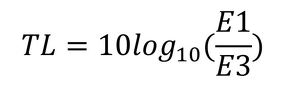 式12
式12