音振動のモデリング 〜実際の製品をモデリングする際のさまざまな手法〜:1Dモデリングの勘所(7)(1/4 ページ)
「1Dモデリング」に関する連載。連載第7回では、引き続き「音振動」のモデリングを扱う。今回は、振動の具体的事例として、流体による構造物の振動のモデリング方法について述べるとともに、振動のモデリングの際に重要な減衰の取り扱いを説明する。さらに、一般的な多自由度系の振動の表現方法と、その具体例としての構造物(梁)の「MKモデリング」に触れ、最後に音振動をエネルギーの流れで捉える方法を紹介する。
前回は振動のモデリングの基本的な方法を説明した。今回は、振動の具体的事例として、流体による構造物の振動のモデリング方法について述べるとともに、振動のモデリングの際に重要な減衰の取り扱いを説明する。続いて、一般的な多自由度系の振動の表現方法と、その具体例としての構造物(梁:はり)の「MKモデリング」に触れ、最後に音振動をエネルギーの流れで捉える方法を紹介する。
流体による構造物の振動
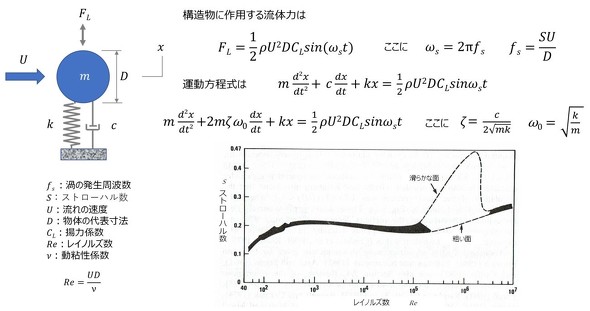
図1に示すように、構造物が流れのある流体中に存在する場合の振動を考える。ここでは、構造物は1自由度系の「MCKモデル」で表現し、2次元形状(奥行方向は単位長さ)と考える。また、構造物の断面形状は円形とする。
この構造物に、左から流速U、密度ρの流体がぶつかると抗力(流れ方向の静的な力、ここでは、これは無視する)の他に、構造物の後流に周期的に渦が発生する。この渦が周期的な揚力となって構造物に作用し、構造物が振動する。これが流体(渦励起)による構造物の振動である。渦の発生周波数fs(Hz)は、構造物の代表長さ(この場合は円の直径)をDとすると、
で表現される。式1のSは「ストローハル数」といわれるもので、構造物の形状、Re(レイノルズ数)によって決まる。図1に円形断面のストローハル数を示す。通常は、約0.2と考えてよい。従って、渦によって構造物が受ける変動力FLは、
となる。ωs=2πfs、CLは揚力係数である。揚力係数もストローハル数と同様に、構造物の形状、レイノルズ数によって決まる(参考文献[1])。ストローハル数、揚力係数は基本的には実験で求めることになるが、最近はCFD(数値流体力学)で予測することも可能になってきている。
以上により、流体から構造物が受ける変動力が定義できたので、図1の構造物の運動方程式は、
となる。後は、通常の振動問題と同様に解けばよい。この場合、渦の周波数と構造物の固有振動数が一致したときに、いわゆる「共振現象」が発生する。ただし、構造物の振動が大きくなると、この振動が流れにも影響し、構造物の振動に渦の発生周波数が影響される「ロックイン現象」なるものが発生する。このような現象をモデルとして予測するのは困難なので、知識として覚えておくことが肝要である。
参考文献:
- [1]R.D.Blevins,Flow-induced Vibration,Van Nostrand Reinhold Inc.,U.S.,1977
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
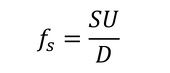 式1
式1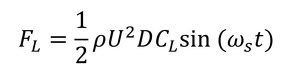 式2
式2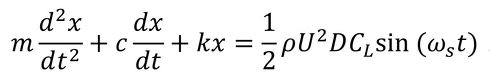 式3
式3