音振動のモデリング 〜実際の製品をモデリングする際のさまざまな手法〜：1Dモデリングの勘所（7）（3/4 ページ）

[大富浩一／日本機械学会 設計研究会，MONOist]

多自由度系の振動

　これまで、構造物を1自由度系の振動モデルで考えてきた。実際には、多くの自由度を有する多自由度系の振動となる。図4に示す通り、2つの質点からなる2自由度系の振動を考えると、運動方程式は各質点に関する2つの式で表現できる。同様の手順で、N自由度を有する振動はマトリクス表示で、

式9

となる。MはN×Nの質量マトリクス（通常は対角行列）、KはN×Nの剛性マトリクス、xはN列の列マトリクスである。N自由度系の固有振動数は、

式10

を解くことで求められる。

図4　多自由度系の振動［クリックで拡大］

構造物（梁）のMKモデリング

　構造物は直接、MKモデルに変換できる場合もあるが、一般的には連続体であることが多いため、これを離散系に変換する必要がある。そこで、連続体の例として梁を考え、この振動問題をMKモデルに置き換えることにする。

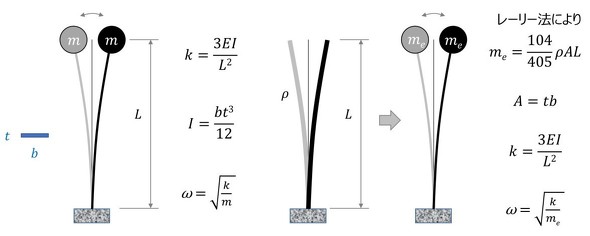
　図5に、2つの梁を示す。図5左図は梁の先端に集中質量があり、梁の質量は無視することが可能だ。この場合、梁の先端に単位荷重を与えた際の変位の式（材力の式）から、等価なばね定数kを定義できる。すなわち、F＝kxでF＝1とし、変位xを材力の式から求めることにより、kを定義できる。

　一方、図5右図のように梁単体の場合には、梁の質量を等価な先端にある質量m_dに置き換える必要がある。その際、「レーリー法」を使うことになる。レーリー法とは“弾性エネルギーと運動エネルギーの合計は一定であり、最大弾性エネルギー＝最大運動エネルギーという関係を利用し、等価質量を算出する”もので、振動モードを仮定する必要がある。

　図5左図の例では、先端に荷重を与えた際の梁のたわみ曲線を振動モードとしたが、図5右図の場合には、自重による梁の静たわみ曲線を用いた方がより正確である。この結果、図5右図の等価質量は（104／405）ρALとなる。すなわち、梁の質量の104／405が先端に集中していると考えることができる。

図5　梁の1自由度系振動モデルへの置換［クリックで拡大］

梁を2自由度系振動モデルへ置き換える

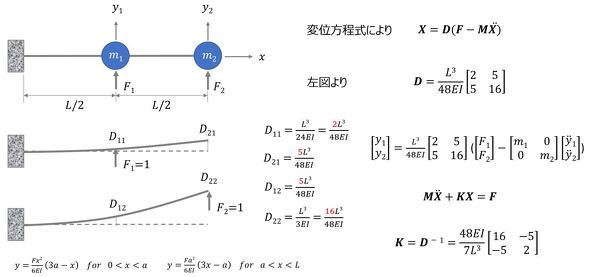
　図5の例では、1次振動モードのみを扱った。実際には、梁が長くなると高次モードも重要となる。図6に、梁を2自由度系振動モデルへ置き換える手順を示す。梁の中間と先端にそれぞれ質点がある梁を考え、これを2自由度系のMKモデルに置き換えることにする。この場合、「変位方程式」で考えると分かりやすい。

　変位方程式とは、各質点に単位荷重を与えた際の各質点の変位をマトリクス表示したものである。図6に示す手順で変位マトリクスDを算出、この逆マトリクスが剛性マトリクスK＝D^-1となる。N自由度系の振動モデルへの置換も同様に行える。多自由度系で図5の1自由度系と同様の方法（「作用方程式」と呼ぶ）をとるには、ある自由度に変位を与えて、その他の自由度は全てゼロ（変位ゼロ）にし、各自由度に作用する力を求める必要があるため、かなり面倒である。

図6　梁の2自由度系振動モデルへの置換［クリックで拡大］

L字梁を2自由度系振動モデルへ置き換える

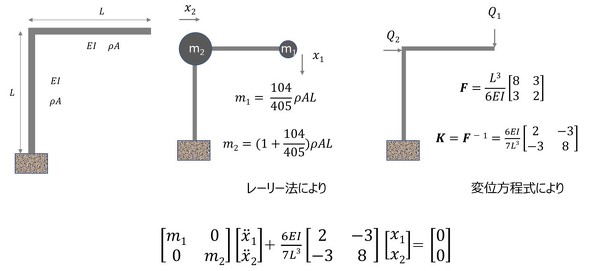
　ここまで説明してきたレーリー法、変位方程式の考え方を用いて、図7に示すL字梁を2自由度系の振動モデルに変換することもできる。ここでは、L字の交差点と先端に等価質量を想定した2自由度系としている。

図7　L字梁の2自由度系振動モデルへの置換［クリックで拡大］