音振動のモデリング 〜実際の製品をモデリングする際のさまざまな手法〜:1Dモデリングの勘所(7)(2/4 ページ)
減衰のモデリング
今まで減衰に関しては、速度比例型の減衰力★(※cxの「x」の上に、時間に関する一階微分の簡易表現であるドット「・」を記載)で表し、減衰定数cで定義した。実際の計算では経験的にこの値を定義、使用しているが、設定根拠が明確ではない。そこで、理論的に減衰を定義する方法を説明する。
前項で流体による構造物の振動について紹介した。この場合、流体抵抗による減衰力が作用する。ここでは、流体が静止している場合の減衰力について考える。図2に示すように、構造物が振動すると、流体から抗力
を受ける。ここでのCDは抗力係数で、形状とレイノルズ数で決まる値である。図2には円柱断面の抗力係数を示す。以降、図1で示した手順で式を展開していくと、最終的に静止流体による減衰は、
となる。すなわち、静止流体による減衰は振動振幅、振動数に比例する。図1のように流体が流れている場合の減衰力も同様に定義できる。以上は、流体が水でも空気でも成立するが、減衰は流体の密度に比例するため、水の方が空気よりも3桁減衰力が大きいことが分かる。
構造物を構成する材料による減衰
次に、構造物を構成する材料による減衰を考える。材料の減衰は損失係数ηで表現され、縦弾性係数などの物性値と同様に、材料ごとに参照できる。通常、減衰を考慮した縦弾性係数は、
と複素表現される。これは、減衰力と弾性力は位相が90度ずれていることから理解できる。なお、損失係数は金属の場合0.001程度である。この考え方にのっとって、図3に示すような通常の減衰と材料減衰を有するばね要素を考えると、この系を支配する運動方程式は、
となる。以降、図3に示す手順で式を展開していくと、最終的に材料による減衰は、
となる。すなわち、損失係数に比例して、振動数に反比例する。なお、共振点ではζm=η/2となる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
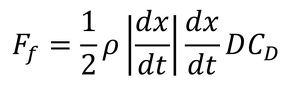 式4
式4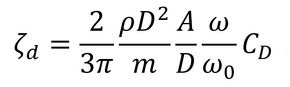 式5
式5
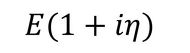 式6
式6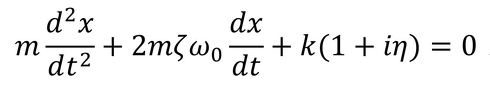 式7
式7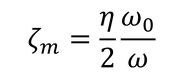 式8
式8






