ラグランジュの方程式(その2)〜ラグランジュの方程式の導出手順と適用例〜:1Dモデリングの勘所(40)(1/5 ページ)
「1Dモデリング」に関する連載。連載第40回では「ラグランジュの方程式(その2)」と題し、ラグランジュの方程式の導出手順とその結果を具体事例に適用して効果を確認する。さらに、ラグランジュの方程式を粘性減衰がある場合に拡張し、実際の問題に適用してみる。
前回は、「ラグランジュの方程式」の基本原理である「仮想仕事の原理」について説明するとともに、グランジュの方程式の基礎となる「一般座標」と「一般力」を紹介した。
今回は、ラグランジュの方程式の導出手順とその結果を具体事例に適用して効果を確認する。続いて、ラグランジュの方程式を粘性減衰がある場合に拡張し、実際の問題に適用してみる。特に、ラグランジュの方程式の導出手順は複雑ではあるが、ラグランジュが苦労、工夫してラグランジュの方程式にたどり着いたプロセスを一度見ておくのも無駄ではないと考える。
ラグランジュの方程式の導出
ある質点系の任意の質点miに作用する力を、平面運動で考えることにし、Xi,Yiとすると、仮想仕事の原理から、
となる。なお、前回の図2で示したような拘束力や振り子の支点の拘束力において、その方向はボールの動きや振り子の動きに直交しているため、このような場合の拘束力による仮想仕事はゼロとなる。だが、ボールの滑走面や振り子の支点に摩擦力が発生する場合、その方向は動きの方向と同じになるため、拘束力には仮想仕事の原理が適用できない。従って、式1は摩擦のある系には適用できない。
式1から、質点系がつり合うための必要十分条件は、任意の仮想変位に対する全ての仮想仕事の代数和がゼロとなることである。これから仮想仕事の原理を動力学系に適用することができる。質点系において、i番目の質点miの運動方程式は、
となる。式2はmiにXi,Yiの成分の外力と、
の成分を持つ慣性力が作用して、つり合いの状態にあることを示している。従って、仮想仕事の原理から、
となり、これから、
となる。ここで、前回示した直交座標表現を一般座標表現に変換する式
を式4に代入する。この式が、δq1,δq2,……のいかんによらず成立するためには、左右両辺のδr(r=1,2,……)の項が等しい必要がある。これより、
となる。
一方、
となり、同様にyiについても
となり、以上の3つの式にmiを乗じて和を取ると、
となる。
一方、Tを系の運動エネルギーとすると、
となる。このとき、
は、一般座標qr、一般速度
の関数であることから、式10から、
が得られる。これは式9の右辺第1項に相当する。さらに、
であるから、この式の両辺を
で偏微分すると、
となる。同様にして、
となる。これらの関係を用いて、式9の右辺第1項は、
となる。式11および式15を式9の右辺に代入し、これを用いて式6を書き直すと、
となる。この式の右辺は、前回の一般座標qrに関する一般力の式
を表すことになるので、
となる。この式でr=1,2,……,nと置けば、n個の独立した方程式を得ることができる。以上の式はラグランジュにより導出されたもので、ラグランジュの方程式と呼ばれる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 品質はどのように作られ、どのように確認されているのか
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 幾何公差の基準「データム」を理解しよう
- 奥行き表現やトラッキング機能を強化したVR設計検証支援システム
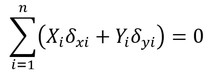 式1
式1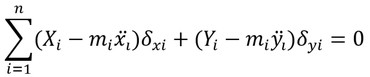 式3
式3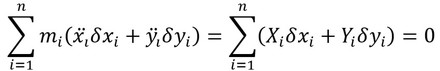 式4
式4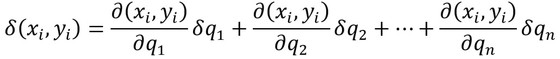 式5
式5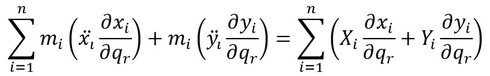 式6
式6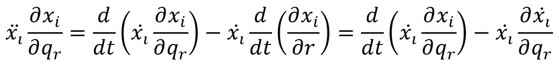 式7
式7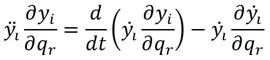 式8
式8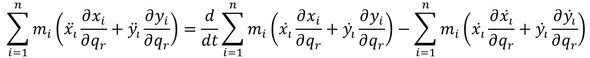
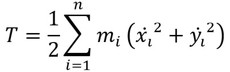 式10
式10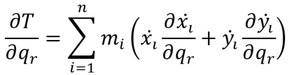 式11
式11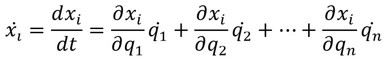 式12
式12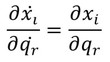 式13
式13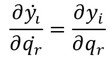 式14
式14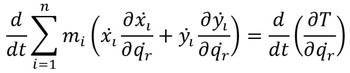 式15
式15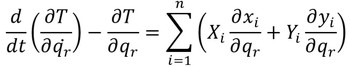 式16
式16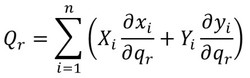 式17
式17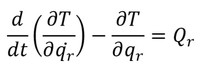 式18
式18





