ラグランジュの方程式(その2)〜ラグランジュの方程式の導出手順と適用例〜:1Dモデリングの勘所(40)(2/5 ページ)
» 2025年02月18日 06時00分 公開
[大富浩一/日本機械学会 設計研究会,MONOist]
一方、保存系において、系の位置エネルギーが力のポテンシャル
の場合、力の成分は、
で与えられる。これを一般力の式に代入すると、
となる。ポテンシャルから導かれる式20の一般力を分離し、その他の成分をQorと置くと、
となり、式18は、
となる。Uは質点の位置により決まり、一般座標qrのみの関数で、一般速度
は含んでいないため、
となる。ここで、
と置くと式23は、
となる。保存系の場合には、Qor=0なので、
となる。Lをラグランジュ関数またはラグランジュアンと呼ぶ。
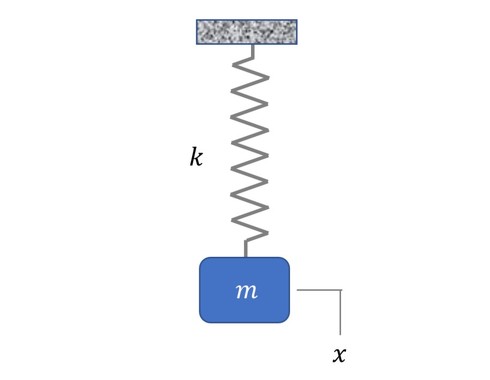
以上を、図1に示す簡単な1自由度系で試してみる。ここで、ラグランジュの方程式は、
となる。このとき、
となり、これを上式に代入して偏微分すると、
を得る。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR
 式20
式20 式21
式21 式22
式22 式23
式23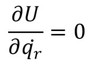 式24
式24 式26
式26 式27
式27 式28
式28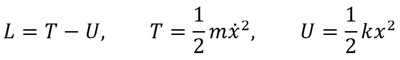 式29
式29