1Dモデリングの方法にもさまざまなアプローチがある:1Dモデリングの勘所(4)(1/3 ページ)
「1Dモデリング」に関する連載。連載第4回では、本題である1Dモデリングの方法を取り上げる。まず、1Dモデリングの方法には大きく「モデル生成」「低次元化モデリング」「類推モデリング」の3つのアプローチがあることを説明。特に本稿では1Dモデリング固有の考え方としての類推モデリングについて詳しく解説する。
連載第1回では、モデリングを製品開発の視点から紹介し、さまざまなモデリングが存在することを示した。連載第2回では、連載第1回の議論を受けて“「1Dモデリング」とは”について考え、続く連載第3回では理論・経験に基づく理論式・経験則(0Dモデリング)が“究極の1Dモデリング”であることを説明した。
今回は、本題である1Dモデリングの方法を取り上げる。まず、1Dモデリングの方法には大きく「モデル生成」「低次元化モデリング」「類推モデリング」の3つのアプローチがあることを説明し、特に本稿では1Dモデリング固有の考え方としての類推モデリングについて詳しく述べる。なお、モデル生成、低次元化モデリングに関してはその概要のみに触れ、詳細については今後の連載の中で事例を用いながら紹介する予定である。
1Dモデリングの方法
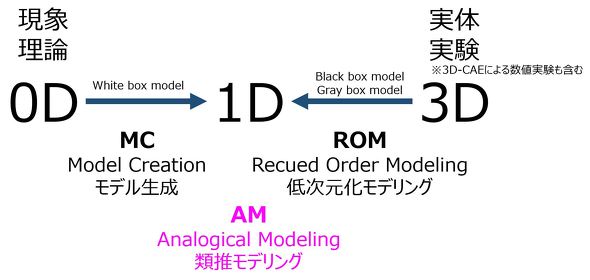
1Dモデリングの方法について図1を用いて説明する。
モデル生成(MC:Model Creation)とは、現象・理論から1Dモデルを作成する方法で連載第3回でも述べたように1Dモデリングが本来目指すところではある。とはいうものの、対象とする現象は多岐にわたり、特に機械系の現象は理論化が容易ではない。
そこで、多く実施されているのが低次元化モデリング(ROM:Recued Order Modeling)である。実体、実験(3D-CAEも含む)からその本質を抽出し、1Dモデルを作成する。
一方、電気系モデルとの対比により類推してモデルを作成するのが類推モデリング(AM:Analogical Modeling)である。類推モデリングは理論に基づいている一方で、現象を単純化して考えるので、図1に示したようにモデル生成と低次元化モデリングとの両側面も有している。
類推モデリング
類推モデリングは一般に「アナロジ」と呼ばれているが、特に決まった方法があるわけではない。通常は、理論が比較的明快な電気系を基本に、各現象を電気系の変数、法則、モデルと対比させて類推する。多種多様な物理現象を同じ土俵で表現する1Dモデリングでは重要な考え方である。しかしながら、きちんとした教科書があるわけはなく、ここでは参考文献[1]を基に、筆者が可能な限り整理した内容を紹介する。
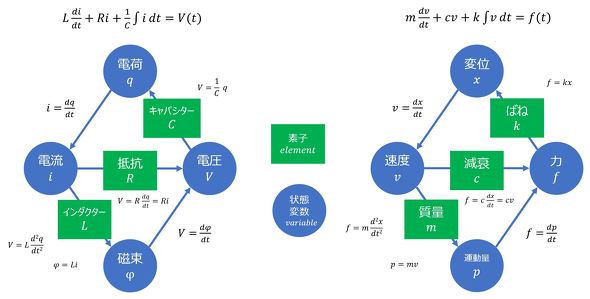
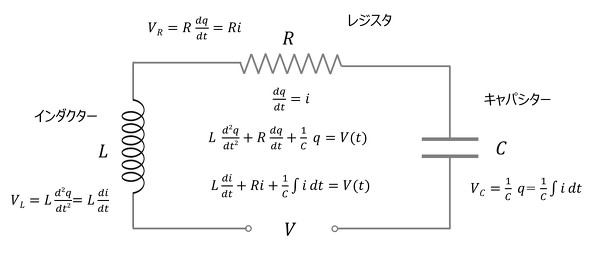
最初に、図2を用いて電気系のモデリングを説明する。ここでは、電気系の3要素であるインダクター(L)、レジスタ(R)、キャパシター(C)が直列につながっており、その両端に電圧(V)が印可されている。なお、qは電荷で、電荷の時間微分が電流iである。このとき、図2の電気系は式1で表現できる。
次に、電気系モデルと機械系(振動系)モデル間の類推について考える。機械系としては次ページの図6右図のmck一自由度振動モデルを考えると、これを支配する方程式は式2となる。
式2は、前述の電気系の式1と同じ形式である。つまり、同じ方法で解けることを意味する。図3に電気系モデルと機械系モデル間の類推を示す。支配方程式が同じだけでなく、要素(素子)同士の関係、変数間の関係も同じ形式で表現できる。
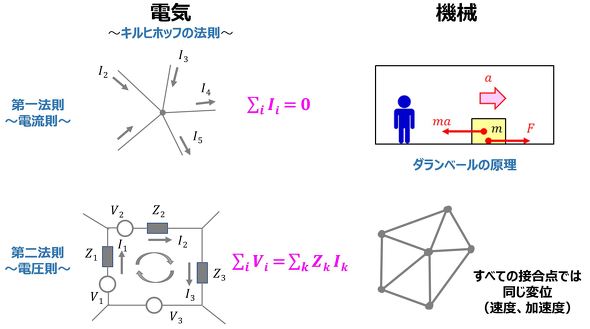
さらに、電気系と機械系の法則間の類推も図4に示すように、「キルヒホッフの第一法則」「ダランベールの原理」「キルヒホッフの第二法則」と、“全ての接合点では同じ変位(速度、加速度)”が対応している。
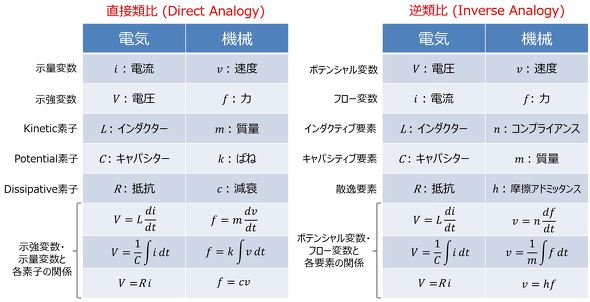
以上を整理した形で、電気系と機械系間の変数の類推として表現したものを図5左図に示す。実は、電気系と機械系の類推には2つの方法があり、以上述べたような方程式の形式から変数、素子(要素)を対応させる方法を「直接類比(Direct Analogy)」と呼ぶ。
一方、変数との類推において、直接類比では電圧(電気系)と力(機械系)を対応させていたところを、電流(電気系)と力(機械系)で対応させることを「逆類比(Inverse Analogy)」と呼ぶ。逆類比では、この変更に伴い、素子(要素)の電気系、機械系間の対応も直接類比とは異なってくる。このように、2つの類推法が存在する理由については以降で説明する。
参考文献:
[1]高橋秀俊の物理学講義、ちくま学芸文庫、2011
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 奥行き表現やトラッキング機能を強化したVR設計検証支援システム
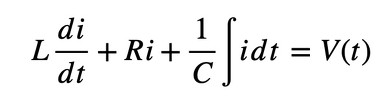 式1
式1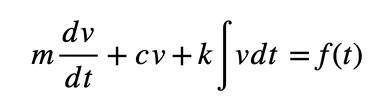 式2
式2