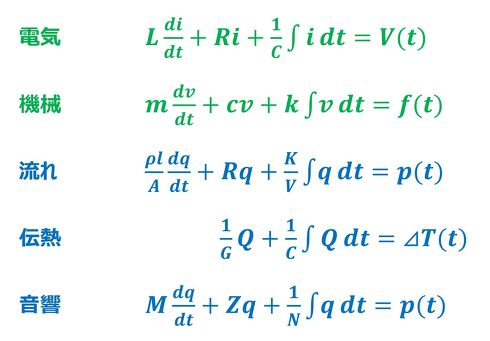　図10にさまざまな現象の常微分方程式表現を示す。各式の説明については今後の連載の中で触れるとし、まずは“方程式の形”に注目いただきたい。このように、種々の現象が同じ形式で表現されていることは、1Dモデリングにおいて強い味方である。ただ、よく見ると伝熱の式には他の式に存在する最初の項が欠落している。本当に存在しないのか、単に見落としているだけなのか、興味は尽きない。このように、1Dモデリングはある意味“創造的なモデリング”ともいえる。

図10　さまざまな現象の常微分方程式表現［クリックで拡大］

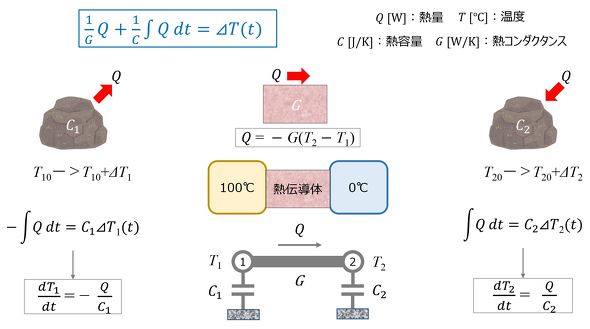
　伝熱の問題を例に、現象の理解、定式化、理論解の一連のプロセスを説明する。図11に対象とする伝熱現象を示す。左側に100℃の物体、右側に0℃の物体があり、両者を熱伝導体（熱容量は無視する）で接続した後の、各物体の温度、流出入する熱量の時間変化を求めることにする。この際、図10の方程式を用いる。

図11　伝熱現象のモデリング［クリックで拡大］

　左の物体からは熱量Qが流出し、温度は低下する。右の物体は熱量Qが流入し、温度は上昇する。熱量Qは熱伝導体を左から右に移動する。左右の物体に関する式と熱伝導体の式の計3つの式が導出できる。知りたいのは、左の物体の温度T₁、右の物体の温度T₂、流出入する熱量Qの3つなので、方程式の数と一致する。

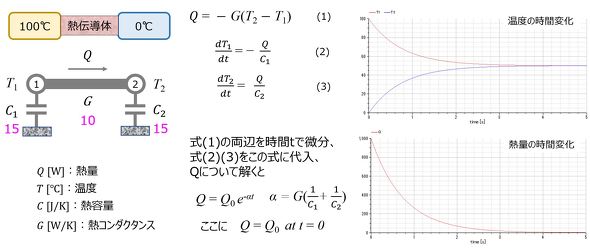
　図12に図11の伝熱現象の理論的解法を示す。ここで、左右の物体の熱容量はそれぞれ15、熱伝導体の熱コンダクタンスは10とした。導出した理論式を示すとともに、結果をグラフで表現した。5秒ほどで左右の物体の温度は同じ50℃になり、熱量も最初の1000［W］から順次低下し、両者の物体が温度平衡に達した5秒後にはゼロとなる。

図12　伝熱現象の理論的解法［クリックで拡大］

低次元化モデリング

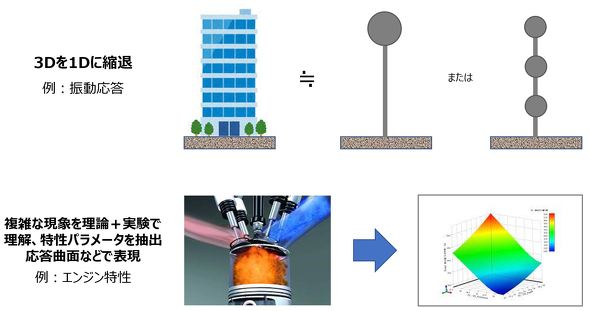
　低次元化モデリングにはさまざまな方法があるが、図13に示すように大きく2つの方法に分けられる。最初の方法は、3Dモデルを1Dに縮退する方法である。図13上図には建物の振動応答モデルの1Dモデリング方法の概念を示す。低次モードだけ知りたい場合には一自由度系のモデルに、高層ビルのように多くのモードが関係する場合には多自由度系のモデルに縮退する。縮退も3D-CAEのモード解析結果を利用する方法や、図のように直接等価剛性、等価質量を求める方法などさまざまある。

　一方、図13下図に示すような複雑な現象の場合には、理論を参考にしながら実験などで現象を理解し、現象の特性を表現するパラメータを抽出して、応答曲面などで表現する。最近は、実験の代替として3D-CAEが活用されている。また、特性式の抽出にディープラーニングなどのAI（人工知能）技術の適用も可能になりつつある。

図13　低次元化モデリングの例［クリックで拡大］

　次回は、類推モデリングの発展形である「熱回路網モデリング」「流体回路網モデリング」について取り上げる。　（次回へ続く）

⇒連載バックナンバーはこちら

筆者プロフィール：

大富浩一（https://1dcae.jp/profile/）

日本機械学会設計研究会
本研究会では、“ものづくりをもっと良いものへ”を目指して、種々の活動を行っている。1Dモデリングはその活動の一つである。

研究会HP：https://1dcae.jp/
代表者アドレス：ohtomi@1dcae.jp

モデリングとは何か？　設計プロセスと製品設計を通して考える
「1Dモデリング」に関する連載。連載第1回は、いきなり1Dモデリングの話に入るのではなく、そもそもモデリングとは何なのか？　について考えることから始めたい。ものづくり（設計）のプロセス、製品そのものを構成する要因を分析することにより、モデリングとは何かを明らかにしていく。
なぜ今デライトデザインなのか？　ものづくりの歴史も振り返りながら考える
「デライトデザイン」について解説する連載。第1回では「なぜ今デライトデザインなのか？」について、ものづくりの変遷を通して考え、これに関する問題提起と、その解決策として“価値づくり”なるものを提案する。この価値を生み出す考え方、手法こそがデライトデザインなのである。
デライトデザインとは？　3つのデザイン、類似の考え方を通して読み解く
「デライトデザイン」について解説する連載。第2回では、デライトデザインとは？　について考える。まず、設計とデザインの違いについて触れ、ユーザーが製品に期待する3つの品質に基づくデザインの関係性にも言及する。さらにデライトデザインを実行する際に参考となる考え方や手法を紹介するとともに、DfXについて説明し、デライトデザインの実践に欠かせない要件を明確にする。
感性設計を基本とした常套的デライトデザインの方法
「デライトデザイン」について解説する連載。今回からデライトデザインの具体的な事例も交えながら理解を深めることとする。連載第3回では、デライトデザインの1つのアプローチとして、「感性設計」を基本とした常套的デライトデザインの方法について、ドライヤーを例に説明する。
「1DCAE」の考え方に基づくデライトデザイン
「デライトデザイン」について解説する連載。連載第6回では、「1DCAE」によるデライトデザインについて詳しく紹介する。まず、1DCAEについて3つのデザインとの関係を含めて説明。次に、デライトデザインに1DCAEを適用する手順について事例を交えて解説する。最後に、技術者に依存するところの大きい価値創出を支援する考え方を取り上げる。
1DCAEの考え方によるカップのデライトデザイン
「デライトデザイン」について解説する連載。連載第7回では、リバース1DCAE⇒1DCAEのカップのデライトデザインへの適用手順を紹介。これにのっとって構造マップの作成、機能マップの考察を実施し、これらを受けて価値を抽出して、価値からアイデアを創出する。さらに、出てきたアイデアの1つについて具現化の方法を考える。