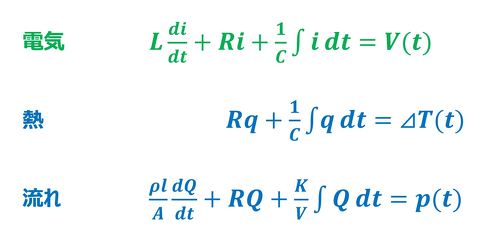　今回は「熱」と「流れ」に着目して、電気との類似性を利用したモデリング方法を説明する。熱と流れは電気回路に置き換えることができ、いわゆる「オームの法則」が成立する。この関係を利用した、熱では「熱回路網モデル」、流れでは「流路網モデル」について、そのモデリング方法と解法を詳しく解説していく。

⇒連載バックナンバーはこちら

熱と流れを電気回路に置き換える

　図1に電気、熱、流れを常微分方程式で表現した例を示す。いずれも類似の形式で表現されるとともに、図示表現した際にも3者の類似性は崩れない。連載第4回の説明では「逆類比（Inverse Analogy）」という概念を導入して電気と機械の類似性を図示表現したが、電気と熱、流れの間の類似性は、「直接類比（Direct Analogy）」や逆類比に関係なく同じ表現形式となる。なお、当然のこと（事実として）であるが、電気（電流）は電圧の高い所から低い所に、熱（熱量）は温度の高い所から低い所に、流れ（体積流量）は圧力の高い所から低い所に流れる。

図1　電気、熱、流れの常微分方程式表現［クリックで拡大］

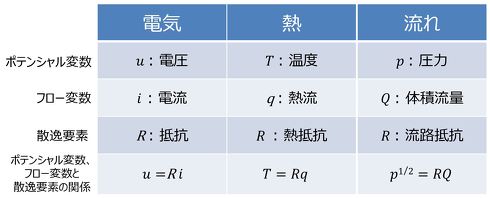
　図2に、電気、熱、流れの類似性を示す。ここでは、逆類比の名称を使用しているが、直接類比でも同じ対応となる。すなわち、電気でいう電圧に対応するのが、熱では温度、流れでは圧力となり、電気でいう電流に対応するのが、熱では熱流、流れでは体積流量となる。そして、散逸要素については、電気では電気抵抗、熱では熱抵抗、流れでは流路抵抗となり、ポテンシャル変数、フロー変数と散逸要素の関係は、電気、熱、流れで対応している。ただし、流れに関しては、“流路抵抗は体積流量の2乗に比例する”ため、少し表現形式が異なってくる。

図2　電気、熱、流れの類似性［クリックで拡大］

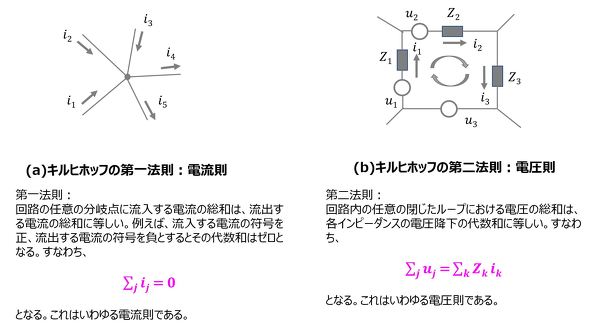
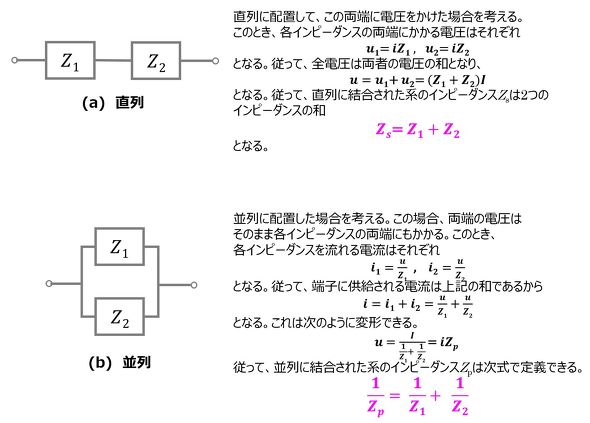
　電気、熱、流れの類似性は、図3のように表現することも可能だ。これは、いわゆる“オームの法則”に相当する。ここでは、物質の移動量がフロー変数に、ポテンシャルの差がポテンシャル変数に対応する。さらに、電気でいうところの図4のキルヒホッフの法則（電流則と電圧測）、図5の等価回路（直列および並列に結合された回路を等価な1つの回路に置き換える）の考え方が、熱と流れにも適用できる。図4と図5では「インピーダンス」という言葉が出てくるが、ここでは単に「抵抗」と置き換えて考えていただきたい。