「熱」と「流れ」を電気回路に置き換えてモデリングする:1Dモデリングの勘所(5)(2/4 ページ)
熱回路網モデル
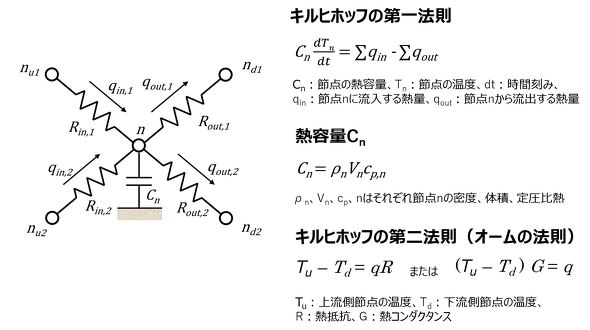
熱回路網モデル(参考文献[1])の考え方を図6に示す。図1で熱は、以下の常微分方程式(式1)で表現できることを示した。
式1の左辺第2項がキルヒホッフの第一法則、第1項がキルヒホッフの第二法則(オームの法則)に対応する。実際の構造物を、熱の流れに沿って、図6のように回路網で離散化することによってモデルを作成する。各節点(図6中のn)では、熱量の流入、流出と、その節点が有する熱量の釣り合い(キルヒホッフの第一法則)から定式化する。一方、熱流路(図6中の抵抗マーク)では、“両端の温度差と熱流は比例する”というキルヒホッフの第二法則(オームの法則)を用いて定式化する。温度差と熱流の比例定数は、熱の伝わりにくさを示す場合には「熱抵抗」を、伝わりやすさを示す場合には「熱コンダクタンス」を使用する。当然のことながら、熱抵抗の逆数が熱コンダクタンスとなる。この逆も同様である。
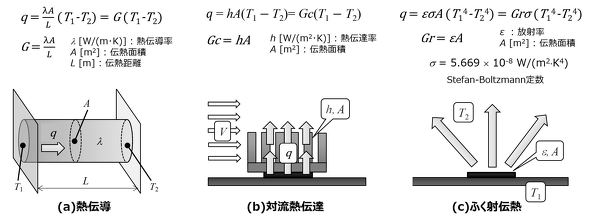
図6の熱抵抗、熱コンダクタンスは熱の伝わり方の形態により、図7のように定義できる。すなわち、熱の伝わり方(熱流の流れ)は「熱伝導」「対流熱伝達」「ふく射伝熱」の3つの形態に分類でき、いずれも図7のように熱コンダクタンスが定義できる。熱伝導は物体内の熱の伝わりやすさで、熱伝達率(物体固有の値)、伝熱面積に比例し、伝熱距離に反比例する。対流熱伝達は空気の移動に伴う熱の移動で、熱伝達率と伝熱面積に比例する。ふく射伝熱は高温物体から低温物体への電磁波を介しての熱のやりとりである。
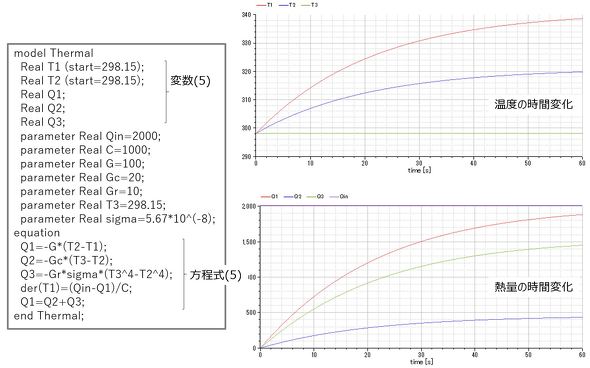
図8は、フライパンを下から加熱した際の熱の流れと、この状態の定式化例を示す。熱はフライパン内部を熱伝導し、フライパン表面から対流熱伝達、ふく射伝熱する。ここで、qinは入熱、T3は外気温、Cはフライパンの熱容量を意味する。そして、温度T1、T2、熱流q1、q2、q3の5つが未知数で、式が5つあるのでこれを解くことができる。
モデルの解法はさまざまであるが、機械系の「1Dモデリング」では、モデリング言語として「Modelica」(参考文献[2])を使用することが多い。Modelicaに関しては今後の連載の中で詳しく解説するが、ここではその適用事例のみを紹介する。図9はフリーソフトの「OpenModelica」(参考文献[3])を用いて、図8の方程式を直接解いた例である。各部温度の時間変化、熱量の時間変化を図9右に示すが、この例では60秒後にある程度フライパンが調理可能な状態(必要温度)に達していることが読み取れる。
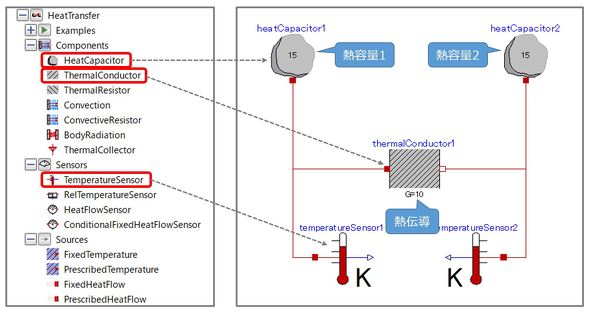
図8は簡単な事例であるので、図9にように直接解くことも可能であるが、複雑な熱の流れを解く場合には、Modelicaの標準ライブラリ「MSL(Modelica Standard Library)」を使用すると便利である。図10に“連載第4回の図12”の事例をMSLでモデル化した例を示す。必要なライブラリをドラッグ&ドロップして結線し、諸元を与えることにより、簡便かつ正確にモデリングを行うことができる。ただし、対象とする現象を正しく理解しておく必要があることは当然である。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
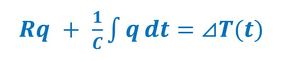 式1
式1