「熱」と「流れ」を電気回路に置き換えてモデリングする:1Dモデリングの勘所(5)(3/4 ページ)
流路網モデル
熱の場合と同様に、流体の流れを“流路”に見立てて流路網モデルとして考える。図1で流れは、以下の常微分方程式(式2)で表現できることを示した。
式2の左辺第1項は流路内の流体の慣性項、第2項は流路抵抗項、第3項はタンクに代表される容量項であるが、ここでは第2項の流路抵抗項について考える。
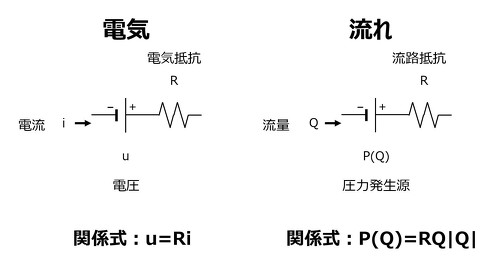
図11に電気と流れの類似性を示す。電気抵抗に相当するのが、流れでは流路抵抗になる。電気では抵抗による電圧降下はRiとなるが、流れでは抵抗による圧力降下(損失)はRQ2となる。圧力損失はこの形式では常に流れの方向に関係なく常に“正の値”となるため、方向性を表現するために「RQ|Q|」と表記する。電気の電圧源に相当するのが、流れでは圧力発生源で、具体的には「ファン」や「ポンプ」といった流体機械のことである。
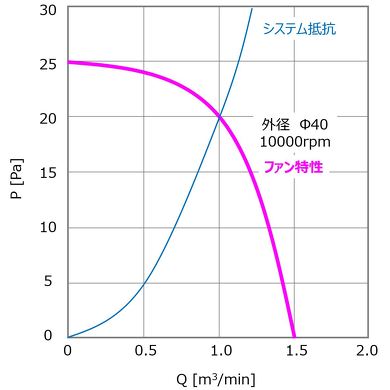
圧力発生源の例として、家電用ファンの特性を図12に示す。横軸に流量、縦軸に圧力をとって、ピンク色の線でファン特性を示す。圧力×流量がパワー(仕事率)である。このファン特性と流路全体の抵抗(システム抵抗:一般的に流量の2乗に比例)の交点が運転点となる。
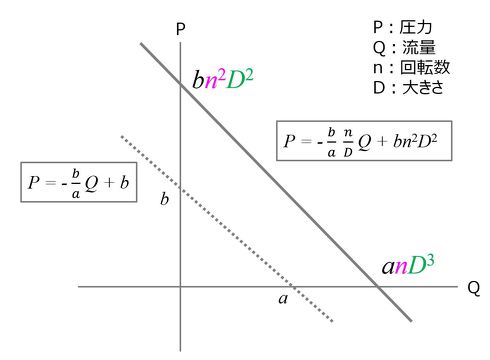
次に、特性を一次近似した場合の圧力発生源のモデリング例を示す(図13)。ここでは、流量は回転数に比例し、大きさの3乗に比例する、圧力は回転数の2乗に比例し、大きさの2乗に比例するという知見を反映している。
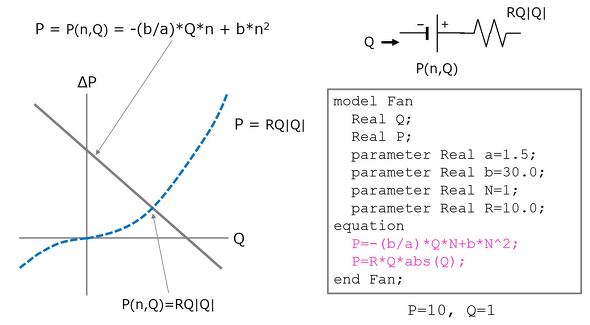
図14に圧力発生源とシステム抵抗の平衡点(運転点)を算出する事例を示す。圧力発生源の特性(回転数も含む)、システム抵抗を与えて、流量と圧力を算出する。
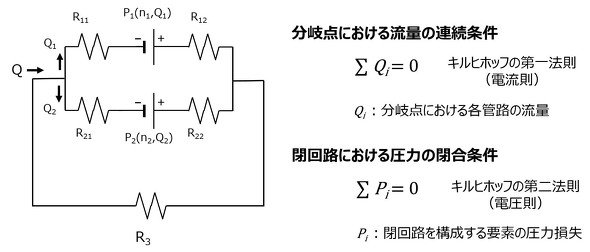
以上の予備検討を経て、図15に示す流路網モデルを作成する。熱回路網モデルと同様に、分岐点における流量の連続条件(キルヒホッフの第一法則)と閉回路における圧力の閉合条件(キルヒホッフの第二法則)を適用する。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
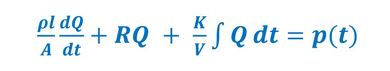 式2
式2