ボルト締め付けトルクと軸力の関係：設計者向けCAEを使ったボルト締結部の設計（4）（4/4 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

ボルト締め付けトルクと軸力の計算例

　では、表1の条件を例にとって計算してみましょう。

	ねじの呼び径：M10	ボルトの種類：六角穴付きボルト
	ピッチ：p=1.5［mm］	有効径：d2＝9.026［mm］
	ボルトの頭の径：Do＝16［mm］	穴径：dh＝11［mm］
	ねじ山の摩擦係数：μth＝0.25［-］	ボルトと被締結体の摩擦係数：μb＝0.25［-］
表1　各種条件

　先ほどの式19に数値を代入すると、トルク係数kは以下の値となり、式1から22.3［Nm］のトルクで締め付けると軸力Fは次の値となります（式20）。

式20

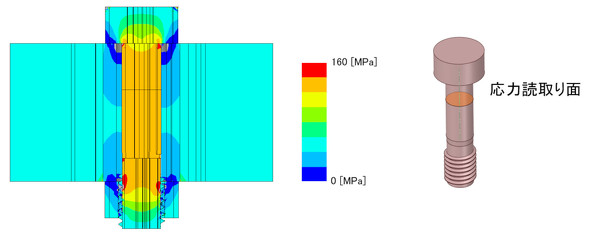
　ここから、いよいよCAEの出番です。モデリングしたらせん状のねじ山を基に、ボルトの締め付けをシミュレーションしてみましょう。解析モデルを図12、図13に示します。

図12　ボルトの締め付け解析モデル ［クリックで拡大］

図13　要素分割図 ［クリックで拡大］

　今回、ねじ山とボルトの軸との結合については節点共有ではなく、接触要素を用いましたので、要素が全て6面体となりました。その代わり、谷底の応力集中は正確には求まりません。ボルトのねじ山とナットのねじ山に摩擦係数0.25［-］の接触要素を配置し、ボルトの頭とボルトの頭に接触する被締結体の面にも摩擦係数0.25［-］の接触要素を配置しました。

　シミュレーションでは、ボルトを10度回転させてその反力となるトルクを読み取りました。図14に軸方向応力分布を示します。図示した面の全ての節点における応力値を読み取って平均値を求め、この応力値に断面積を乗じることで軸力を求めました。

図14　軸方向応力分布 ［クリックで拡大］

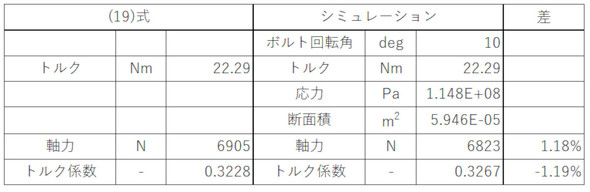
　表2に計算結果をまとめます。

表2　ボルト軸力の計算：理論式とシミュレーションの比較 ［クリックで拡大］

　同じ締め付けトルクに対して発生する軸力は約6900［N］で、理論式とシミュレーションとの差は1.18％となり、よく一致しました。理論式の導出では、図3、図4で示したようにいくつか迷うところがありました。シミュレーションでは全てのパーツを弾性体としたので、図3で述べたナットの弾性変形も考慮されています。結果、両者が一致したことで、これで正しかったのではないかとほっとしています。

---

　今回は、ボルト締め付けトルクと軸力の関係式の導出に終始しましたが、この関係式は、ボルトが疲労破断しない条件を満たすかどうかの判定に必須となりますし、締め付けトルクを自分で決めるときにも使うため、とても重要です。

　次回は、摩擦係数について実験データを紹介します。摩擦係数が分かったら、締め付けトルクの決定法を述べ、そして、最終目標である設計者CAEを用いた締結部の設計方法を解説します。　（次回へ続く）

⇒「連載バックナンバー」はこちら

Profile

高橋 良一（たかはし りょういち）
ＲＴデザインラボ 代表

1961年生まれ。技術士（機械部門）、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ