ボルト締め付けトルクと軸力の関係:設計者向けCAEを使ったボルト締結部の設計(4)(3/4 ページ)
ボルト締め付けトルクと軸力の関係
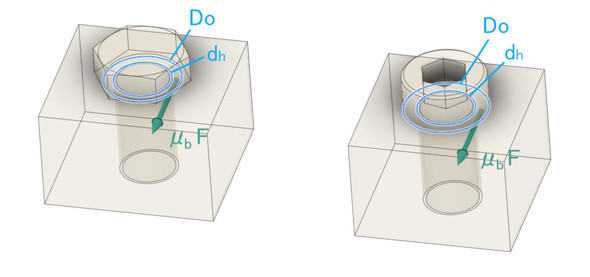
式11は、ねじ山に発生する摩擦力だけを考慮していましたが、ボルトの締め付けではボルト頭と被締結体とに発生する摩擦力を考慮しなければなりません。摩擦力の円周方向成分を図11のμbFで表します。
dhはボルト穴径、Doは六角ボルトの場合では被締結体と接している面の外径、六角穴付きボルトの場合ではボルト頭の直径になります。μbFは円周方向に作用するので、その直径Dbを求めなければなりません。Dbは、dhとDoの間にあります。参考文献[2]によると式12となります。
参考文献:
- [2]吉本勇、ねじ締結体設計のポイント、日本規格協会、(2002)
一方、JIS B 1083(参考文献[3])によると式13となります。
参考文献:
- [3]JIS B 1083、ねじの締め付け通則、(2008)
ここでは式13を採用しましょう。ボルト頭と被締結体とに発生する摩擦力を考慮したボルト締め付けトルクと軸力の関係は式14となります。
ここまでの解説を読んで、「おやっ? 自分が使っている式やJISの式と違っているぞ」と思われたかもしれません。式を変形していきましょう。式8に戻り、これを上式に代入します(式15)。
式2を使ってβを計算すると、およそ0.05[rad]と1よりもはるかに小さい値となります。このようにβが微小なとき、三角関数は式16で近似できます。ただし、βの単位はラジアンであることに注意してください。
式5において、cos β≅1とすれば、α≅α’となります。せっかく、図7を作図したのに少し残念です。そして、tan βが微小なので式15の分母第2項を無視すると式17となります。
これで、かなり多くの方が使っている式になりましたね。式2を代入すると、αは30度になるので、cos α=0.866を代入すると式18が得られます。
式1を使ってトルク係数を求めてみましょう。
JIS B 1083(参考文献[3])の式になりました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

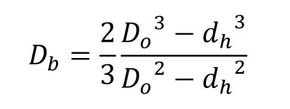 式12
式12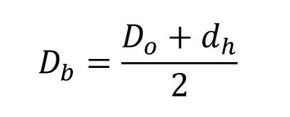 式13
式13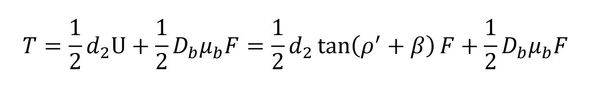 式14
式14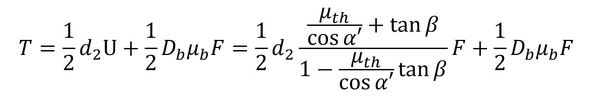 式15
式15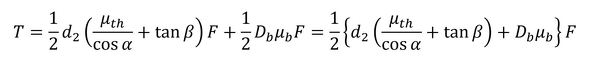 式17
式17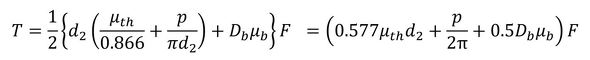 式18
式18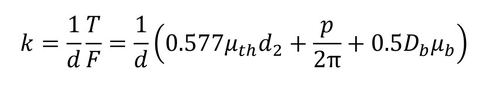 式19
式19





