ボルト締め付けトルクと軸力の関係:設計者向けCAEを使ったボルト締結部の設計(4)(2/4 ページ)
ねじ面におけるトルクと軸力の関係(2)
これから力の釣り合い式を立てて、これを解いてトルクと軸力の関係を導くのですが、反力Vが傾いています。Vを半径方向成分、円周方向成分、軸方向成分に分解する必要があります。
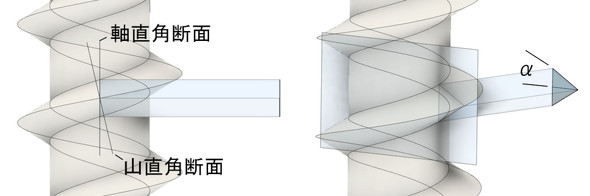
その前に、ねじ山のフランク角αについて述べます。図6はフランク角αの定義です。αは、ねじ山の軸直角断面で定義されていて、30度です。
一方、反力Vはねじ面に垂直なので、図2の右側の図ではリード角βだけ傾いています。Vの力の分解では、βだけ傾いた面である山直角断面で考える必要があります。山直角断面では、フランク角は少しだけ小さくなります。α’で表記します。αとα’の関係を求めておきましょう。
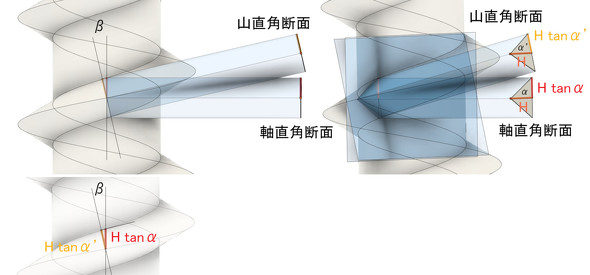
図7にフランク角の関係を示します。ねじ山の高さH寸法は、軸直角断面と山直角断面で等しいです。右側の図のH tan αとH tan α’の長さを比べます。図7左下の図から次式(式4、式5)が成立します。
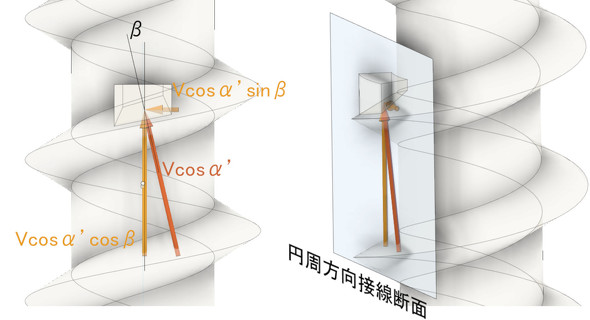
いよいよ反力Vの分解です。図8の山直角断面で考えます。反力Vは、V cos α’とV sin α’に分解されます。V sin α’は、図2のRと釣り合うことになります。
山直角断面で分解したV cos α’を、今度は円周方向接線断面上で分解します(図9)。V cos α’は、V cos α’ cos βとV cos α’ sin βに分解されます。
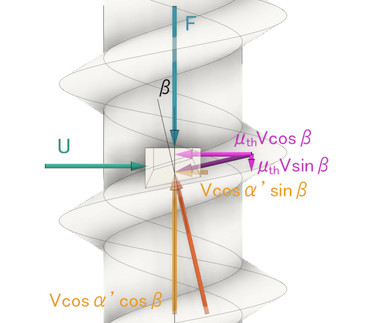
図10に、軸力F、円周方向接線力Uと、摩擦力μthVを分解したμthV cos βとμthV sin βを追記しました。これで役者がそろいました。
軸方向と円周方向の力のつり合い式を立てます(式6、式7)。
式6、式7からVを消去して、
となります。
次に、摩擦角ρ’を式9で定義します。
すると、先ほどの式8は式10のようになり、かなりすっきりとします。
そして、式10を式2に代入すると、ねじ面におけるトルクと軸力の関係が求まります。式11は多くの文献に載っています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

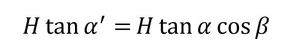 式4
式4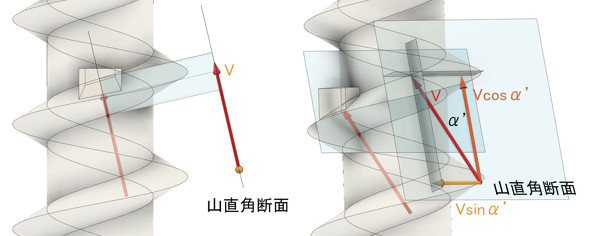
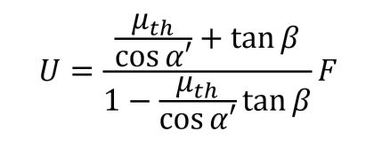 式8
式8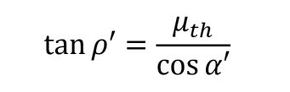 式9
式9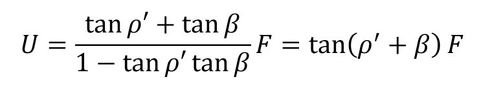 式10
式10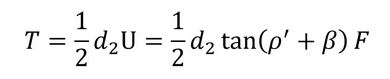 式11
式11





