ボルト締め付けトルクと軸力の関係:設計者向けCAEを使ったボルト締結部の設計(4)(1/4 ページ)
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第4回では「ボルト締め付けトルクと軸力の関係」を導きます。
連載第3回で「ボルトが疲労破壊しない条件は、変動荷重が作用したときに締結体同士が離れないこと」、そして「そのためには大きな締結力、つまりボルト軸力が必要だ」と述べました。
締結部の設計では“軸力の見積もり”が必要です。締め付けトルクを大きくすると軸力も大きくなります。ということは、必要な軸力を発生させるための締め付けトルクの計算が必要になります。締め付けトルクT[Nm]と軸力F[N]の関係は、式1で表せます。
- d:ねじの呼び径[m]
- k:トルク係数[-]
トルク係数はWeb検索すればすぐに出てきます。どうやら0.15〜0.2[-]が一般的な値のようですが、少し幅がありますね。これをうのみにするのではなく、自分で計算できるようになりましょう。
また、レビュー時の関係者や顧客からの「締め付けトルクは?」の問いに対して、「はい、今回はT系列を採用しましたが、これはいわゆる弾性締め付けで、締め付け時のボルトの応力が降伏応力の約70%になるような値としています」と言い切るためには、締め付けトルクから軸力とボルト軸部に発生している応力の両方を計算しなければなりません。ということで、今回はボルト締め付けトルクと軸力の関係を導きます。
ねじ面におけるトルクと軸力の関係(1)
ねじ面におけるトルクと軸力の関係は参考文献[1]に記載されていますが、違う方法で導きましょう。
参考文献:
- [1]山本晃、ねじ締結の理論と計算、養賢堂、(1975)
図1に解析モデルを示します。まず、リード角β[rad]を説明します。リード角は式2で定義されます。
- p:ピッチ[m]
- d2:ねじの有効径[m]
解析モデルでは、めねじの一部分を取り出しています。これを「微小めねじブロック」と呼ぶことにします。微小めねじブロックに円周方向接線力Uが作用しているとします。トルクT[Nm]は式3で表されます。
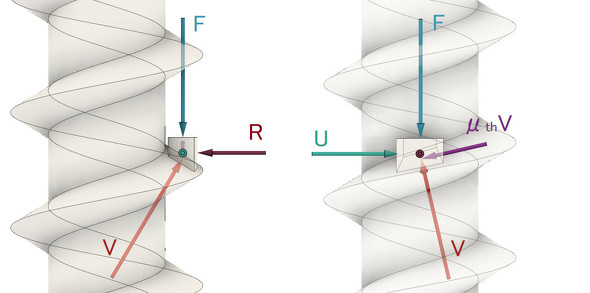
トルクTによって軸力Fが発生します。UとFの関係を導きましょう。おねじ山から微小めねじブロックに作用する力は、ねじ面に垂直な力Vと、Vによる摩擦力μthVです。μthは、ねじ面間の摩擦係数です。摩擦力μthVは接触面と平行で、かつ今まさに動こうとする方向と反対の方向に発生するので、円周接線方向からβだけ傾いた方向に発生します。図2のようなイメージでしょうか。
図2を作図しながら「おやっ」と思いました。図3に示すように微小めねじブロックは、ねじ山を滑り落ちようとするため、ナットが弾性変形して半径方向に少しだけ膨張します。つまり、弾性変形時に微小めねじブロックは、図3の矢印方向に移動することになります。摩擦力は「今まさに動こうとする方向と反対の方向に発生する」と述べました。すると、摩擦力の成分として図3の矢印の反対方向に発生する成分も発生することになります。
図2において、反力Vの方向は接触面と垂直なので疑う余地はないのですが、摩擦力の方向については勝手に決め付けていたようです。摩擦力はVと垂直ですが、図4に示すようにいろいろな方向が考えられます。
送りねじの場合、ねじを回し始めた瞬間に軸力はゼロからFまで上昇し、ナットは弾性変形しますが、その後Fは一定となりナットは弾性変形後の形を維持するので、もはや微小めねじブロックは図3の矢印方向に移動しようとしません。よって、この図3の矢印の反対方向に発生する摩擦力の成分は発生しません。しかし、ねじ締め付けでは、軸力Fは時々刻々と上昇するので、弾性変形量も同様に増加して微小めねじブロックは図3の矢印方向に動こうとするのではないでしょうか。この結果、摩擦力の方向が変わるかもしれません。
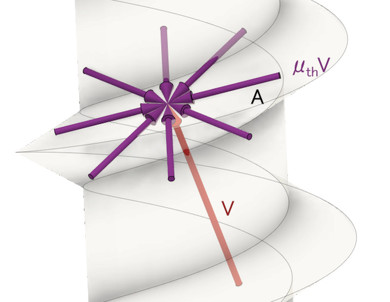
では、ボルトが回転しているときの微小めねじブロックの移動方向をベクトルで考えてみましょう。図5に微小めねじブロックの移動方向を示しました。
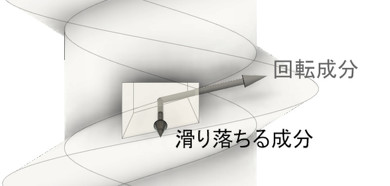
微小めねじブロックの移動方向は、回転成分と滑り落ちる成分とのベクトル和と考えられます。滑り落ちる成分は弾性変形なので非常に小さい値ですが、回転成分はそれなりの値を持っています。この結果、ベクトル和は“ほぼ回転成分と同じ”と考えられます。というわけで、摩擦力の方向は図4のA、つまり円周の接線方向と考えてよさそうです。しかし、回り始める瞬間は回転成分と滑り落ちる成分がゼロなので、摩擦力の方向がクルッと変わってしまうかもしれませんね。今回はボルトが回転しているときを考えることにするので、摩擦力の方向は図4のAを採用することにしましょう。図2に変更はありません。お騒がせしました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 【レベル9】アセンブリ図面を作成せよ!
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 品質はどのように作られ、どのように確認されているのか
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 幾何公差の基準「データム」を理解しよう

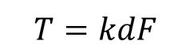 式1
式1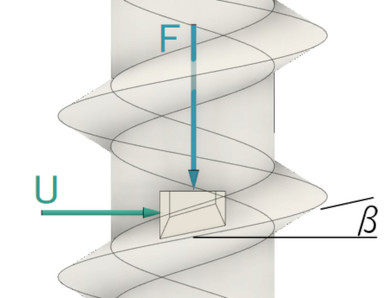
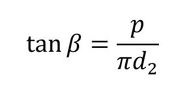 式2
式2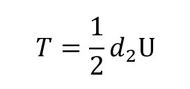 式3
式3