ボルトが疲労破壊しない条件:設計者向けCAEを使ったボルト締結部の設計(3)(1/4 ページ)
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第3回は「ボルトが疲労破壊しない条件」について詳しく取り上げる。
最初に結論からお伝えします。「ボルトが疲労破壊しない条件は、変動荷重が作用したときに被締結体同士が離れないこと」です。
このためには、大きな締結力、つまりボルト軸力が必要です。ボルトの強度区分は、3.6〜12.9まであって、引っ張り強さは300〜1200[MPa]まであるのですが、ボルトが疲労破壊したからといって、締め付けトルクを変えずにボルトの強度区分を上げるだけでは対策になりません。対策には大きな軸力が必要です。
疲労の対策は、素材の強度向上が寄与しているのではなく、締め付け力向上が寄与しているのです。軸力向上の手段として締め付けトルク向上があり、締め付けたときにボルトを破断させないためにボルトの強度区分を上げるのです。
それでは、ボルトが疲労破壊しない条件を導いていきましょう。いよいよ設計者CAEの出番となります。
ボルトと被締結体のばね定数
ボルトには、締め付けトルクによって発生する「平均応力」と、部品(被締結体)に作用する荷重(変動荷重)による「応力振幅」が発生します。応力振幅が連載第2回で述べた疲労強度より小さければ、ボルトは疲労破壊しません。
疲労破壊の有無の予測のためには、ボルトに発生する応力振幅を見積もる必要があり、この手段として「締め付け線図」があります。締め付け線図では、ボルトと被締結体のばね定数を求めておく必要があります。早速やってみましょう。
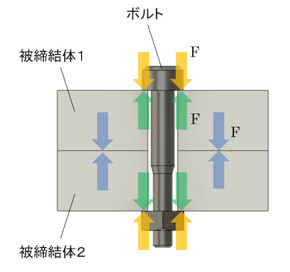
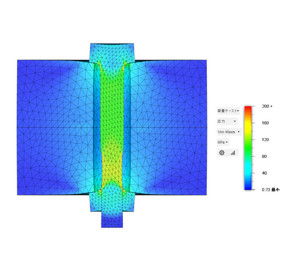
図1のようなモデルを考えます。初期状態では、ボルトを締め付けたことによってボルトに軸力Fが発生し、ボルトの頭は被締結体をFなる力で押し付けています。被締結体は、上からはボルトによってFなる力で押され、下方からはナットによってFなる力で押されています。被締結体1と被締結体2もFなる力で押し合っています。ギューッと押されている感じを解析してみました(図2)。
図1と図2の状態で、ボルトはλbだけ伸びていて、被締結体はλpだけ縮んでいるとしましょう。添え字のbはboltの“b”、添え字のpはpartsの“p”です。F、λb、λpの関係は式1、式2で表すことができます。
Kbはボルトのばね定数、Kpは被締結体1と被締結体2のばね定数です。Kbは、以下の式3〜5によって見積もることができます(参考文献[1])。
- Eb:ボルト材のヤング率[Pa]
- d:ねじの呼び径[m]
- d3:ねじの谷径[m]
- La、Ls:図3に示す長さ[m]
Kpは、式6で計算できます(参考文献[1])。
- Ep:被締結体のヤング率[Pa]
- Lf:図3に示す被締結体の長さ[m]
- D:被締結体の外径[m]
- dw:ボルト頭の直径[m]
- D1:ボルト穴径[m]
- Dm:圧縮変形が等価であるような中空円筒の直径[m]
今回はD>3dwなので、式7で計算できます。
参考文献:
- [1]:吉本勇:ねじ締結体設計のポイント:日本規格協会(2002)
M10のステンレス製ボルトで計算してみましょう。同時に設計者CAEの範疇(はんちゅう)、つまり単品解析でばね定数Kb、Kpを求めてみましょう。
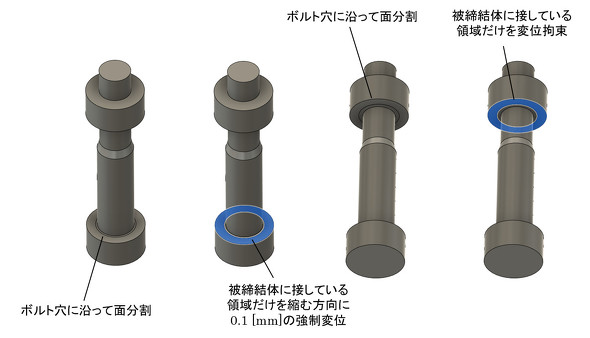
まず、ボルトのばね定数Kbを求める解析条件を図4に示します。ボルト頭の面とナットの面をボルト穴に沿って面分割しています。細かいことですが、式3のかっこ内第1項と第4項は、ボルトの頭とナットの変形を考慮した成分ですので、解析モデルもそれらを考慮しました。
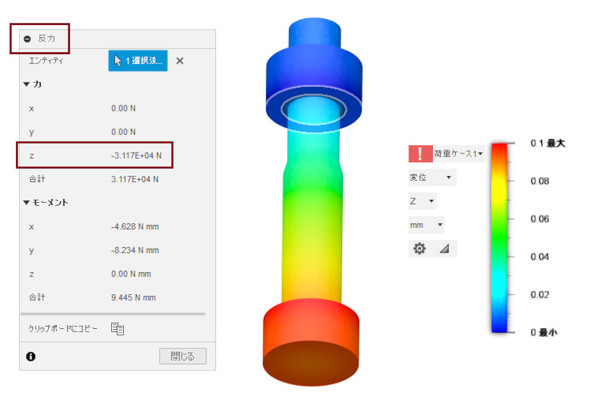
図5に解析結果(変位図)を示します。必要なのは、強制変位させた面に作用する反力ですので、これを表示させます。3.117×104[N]となりました。強制変位量は0.1[mm]だったので、Kbは3.117×105[N/mm]となりました。
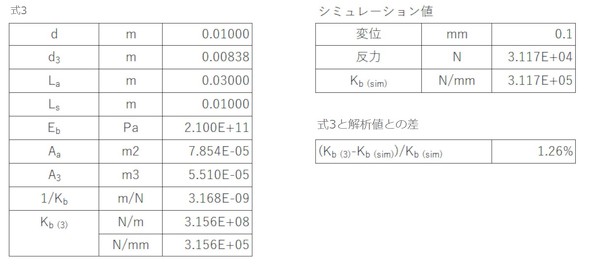
式3の計算結果および式3によるKbと解析によるKbの差を表1に示します。差は、1.26%とまずまずの結果となりました。
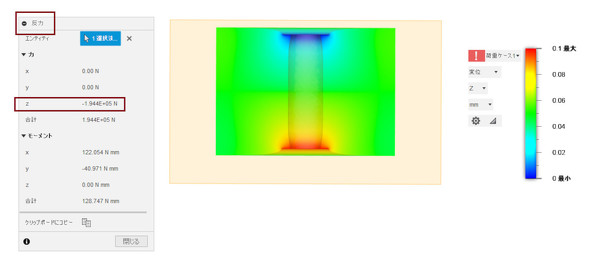
次に、被締結体のばね定数を求めましょう。境界条件は同様なので、解析結果を図6に示します。
強制変位に対する反力は、1.944×105[N]となったので、ばね定数Kpは1.944×106[N/mm]となりました。式6によるKpと、解析によるKpを表2に示します。式6の計算結果は1.150×106[N/mm]となり、差は40.82%となりました。
差が出た理由を考察しましょう。式6では、圧縮変形が等価であるような中空円筒のばね定数を求めています。一方、図6の変形図では、ボルトの頭とナットとの接触面が陥没しています。等価な中空円筒による近似では無理があるかもしれません。これらの式の元は「VDI(Verein Deutscher Ingenieure) 2230」で、ドイツ技術者連合が推奨している式です。Kpの見積もりはCAEを使った方がよさそうです。
ここで注目しておきたいのは、KbとKpには約6倍の開きがあるということです。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

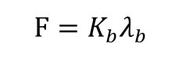 式1
式1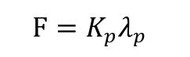 式2
式2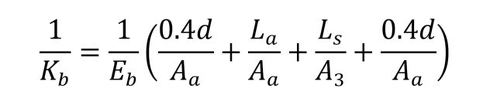 式3
式3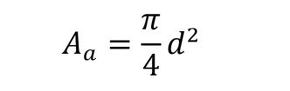 式4
式4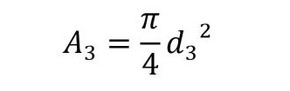 式5
式5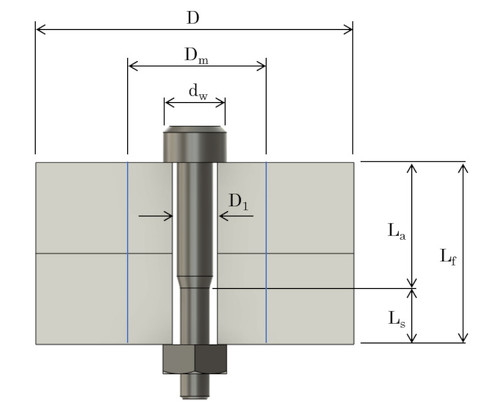
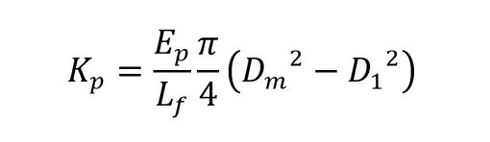 式6
式6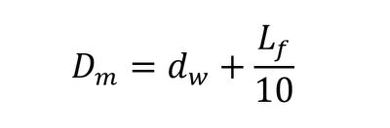 式7
式7