ボルトが疲労破壊しない条件:設計者向けCAEを使ったボルト締結部の設計(3)(2/4 ページ)
ボルト締め付け線図
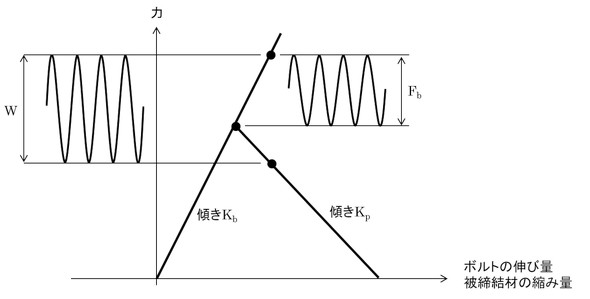
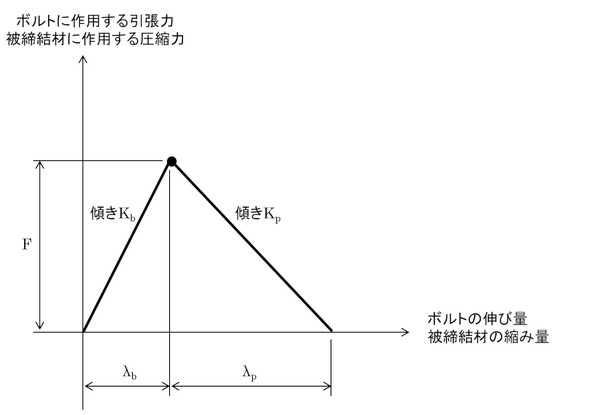
ばね定数が求まりましたので、締め付け線図を作成しましょう。前ページに示した図1の初期状態を考えます。ボルトはλbだけ伸びていて、被締結体はλpだけ縮んでいるとしました。F、λb、λpの関係は式1、式2で表しました。この状態の締め付け線図を図7に示します。線図の傾きはばね定数となります。
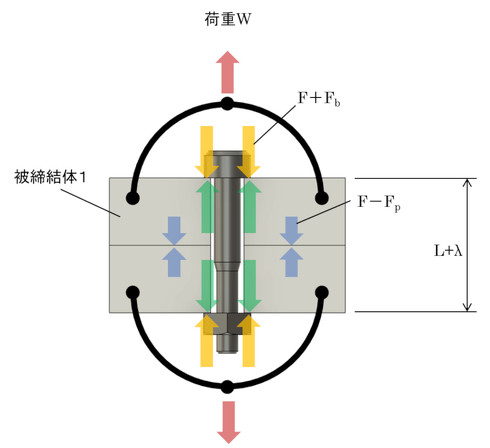
続いて、被締結体に荷重Wが作用している状態の力関係を図8に示します。
被締結体1に作用する力に注目します。荷重Wによって上方向に引っ張られるので被締結体1と被締結体2が押し合っていた力は「F−Fp」に減少します。被締結体1が上方向に引っ張られたのでボルトが下方向に押す力は「F+Fb」に上昇します。このとき被締結体1と被締結体2の合計長さLは、λだけ伸びるという考えはとても自然な発想です。これに従いましょう。つまり、ボルトはλだけ伸びて、被締結体もλだけ伸びるのですが、被締結体は初期状態でλpだけ縮んでいるため、被締結体の縮み量は「λp−λ」になると考えられます。
被締結体1の上下方向の力のつり合いを考えます(式8、式9)。
ボルトの伸びλと被締結体の縮み量の変化量λを考慮して、荷重Wが作用した状態の締め付け線図を図9に示します。
変動荷重が作用したときのボルトに発生する応力振幅が関心事なので、FbとWの関係を求めましょう。図9から式10、式11が成立することが分かります。
式10と式11を、式9に代入すると式12が導かれます。
式10に式12を代入します(式13)。
Φは式14で定義され、「内力係数(または内荷重比)」と呼ばれる量で、Φを用いてボルトに発生する変動荷重が求まります。
ついでに、Fpを求めると式15となります。
以上で、FbとWの関係が求まりました。
ボルトに発生する変動荷重【その1】
荷重Wが、0〜Wまで変動する場合を考えてみましょう。ボルトに発生する変動荷重は図10のようになります。締結面が離れなくても、ボルトには案外大きな変動荷重が発生しそうです。
ここまでは多くの書籍で述べられています。ここから本論になります。
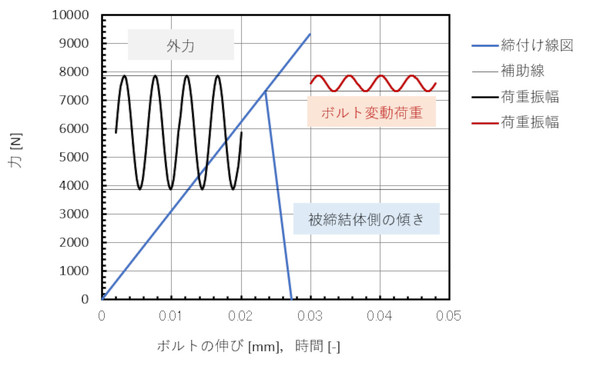
ボルトと被締結体のばね定数について取り上げた際、ばね定数を見積もり、KbとKpに「約6倍の開きがある」と述べました。内力係数Φを0.138[-]として、グラフに数値を代入しましょう。図11のようになります。
ここではM10ボルト、締め付けトルク24.5[Nm]、摩擦係数0.26[-]としました。図11から、ボルトの変動荷重幅(最大値−最小値)を読み取ると、つまり式13で求まる値は552.7[N]となります。この値は覚えておいてください。
KbとKpを比べると、圧倒的にKpが大きく、締め付け線図の被締結体側の傾きは、多くの文献で図10のように描かれているのですが、実際はそのようなものではなく、被締結体の傾きはとても急峻(きゅうしゅん)なのです。
この結果、ボルトに作用する変動荷重はとても小さくなって、応力振幅も小さくなり、ボルトの繰り返し荷重に対する耐性が強いものになるのです。連載第1回で、「ボルトが適切なトルクで締め付けられていれば、ボルトは疲労に対して案外タフだ」と述べた理由はここにあります。実は、ボルトに発生する応力振幅はもっと小さくなります。有限要素法の出番です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

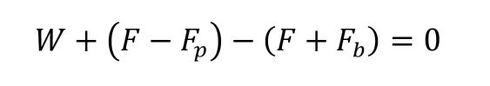 式8
式8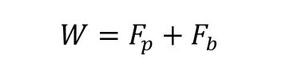 式9
式9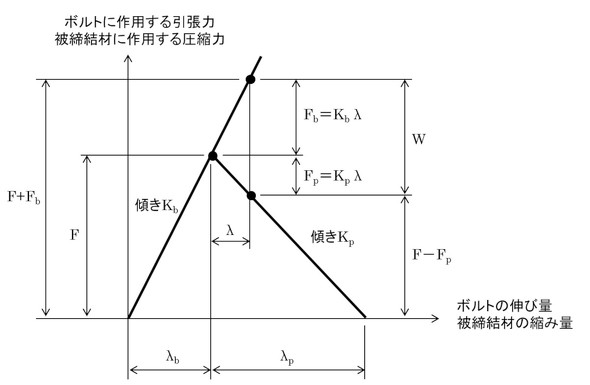
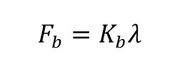 式10
式10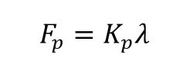 式11
式11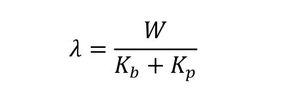 式12
式12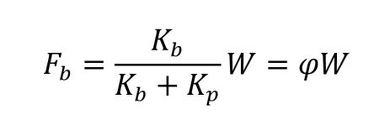 式13
式13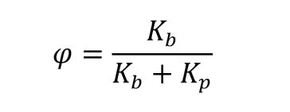 式14
式14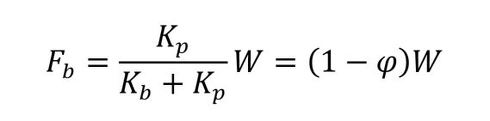 式15
式15