ボルトが疲労破壊しない条件：設計者向けCAEを使ったボルト締結部の設計（3）（3/4 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

ボルトに発生する変動荷重【その2】

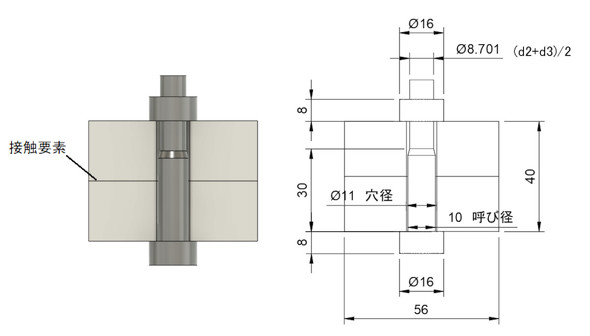
　ボルトに発生する応力振幅を、有限要素法で求めてみましょう。図12のようなモデルでボルトに発生する応力振幅を求めます。このモデルは参考文献［2］を参考にしました。参考文献［2］は、比較的新しい論文でとても参考になります。

図12　解析モデル ［クリックで拡大］

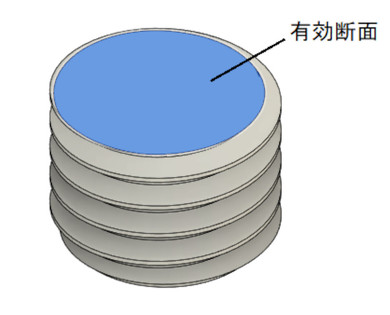
　ボルトのねじ部の直径は、谷径d₃と有効径d₂の平均値としています。図13は、ねじ部の断面ですが、ねじの断面積は谷径を直径とした円の面積より大きいので、このような近似を行いました。この直径による面積を「有効断面積」と呼びます。余談ですが近似をしなくても3D CADでは面積が直接求まりますね。そして、今回は設計者CAEの範疇から外れて接触要素を使いますが、最終的に提案する方法は“接触要素を使いません”のでどうぞご安心ください。

図13　ねじの有効断面 ［クリックで拡大］

　ボルトの締め付けトルクはT系列を採用し、24.5［Nm］としました（参考文献［3］）。なお、ボルトの締結トルクの決定方法については以降の連載の中で説明しますので、このトルクの妥当性に関してはそれまでお待ちください。

参考文献：

• ［2］：萩原正弥：ねじの疲労破壊、精密工学会誌（2015） Vol.81 No.7 P623
• ［3］：東日製作所Webサイト

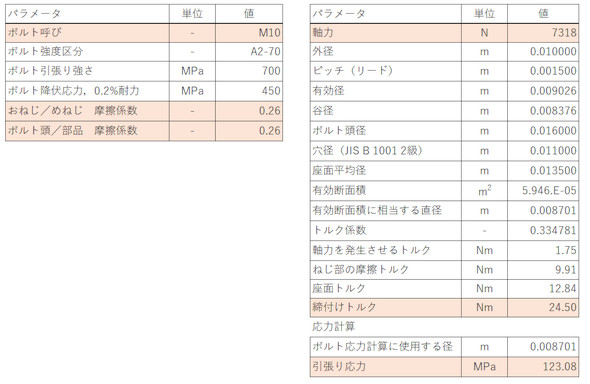
　ボルトに発生する軸力は、表3のように計算しました。「ボルトが疲労破壊しない条件は被締結体同士が離れないこと」だったので、設計計算では厳しめに見積もって（悲観的に考えて）、軸力が小さな値になるような条件で計算します。よって、摩擦係数は大きめの0.26［-］としました。摩擦係数を0.26［-］とした理由もいずれ説明します。軸力は7318［N］となりました。この軸力を有効断面積で割った応力（初期締結時の応力）は123.08［MPa］です。軸力の計算方法は次回説明します。

表3　ボルトの軸力の計算 ［クリックで拡大］

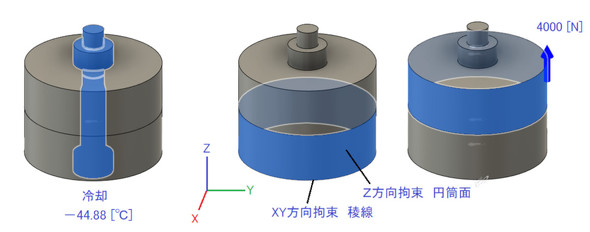
　境界条件を図14に示します。7318［N］の軸力を発生させるためにボルトとナットを20［℃］から−44.88［℃］に冷却しました。下側被締結体の円筒面のZ方向の移動を拘束し、上側被締結体の円筒面に対してZ方向に4000［N］の荷重を加えました。つまり、「W＝4000［N］」ということになります。上側被締結体と下側被締結体との間には、“摩擦あり接触要素”を配置しました。

図14　境界条件 ［クリックで拡大］

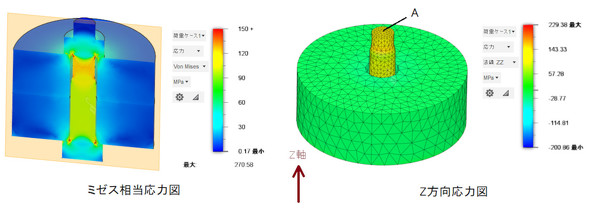
　図15に解析結果を示します。ボルト頭部に応力集中が発生していますが、ボルトの疲労破壊は雌ねじとかみ合う第1山の谷底から発生しますので、今回は検討から除外します。ここでは、Z方向垂直応力（ボルト軸方向応力）で評価します。図15右側のA面上の全ての節点の応力値を「Excel」に読み込み、平均値を求めました。荷重作用時のボルトの応力は123.77［MPa］となりました。一方、初期締結時の応力は表3から123.08［MPa］なので、その差は0.69［MPa］となりました。これに有効断面積を掛けるとボルト変動荷重になり、40.97［N］が求まります。

図15　解析結果 ［クリックで拡大］

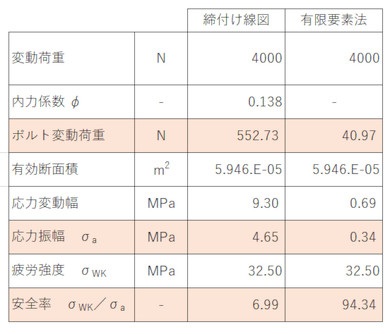
　先ほど「この値は覚えておいてください」といった、締め付け線図から求めたボルト変動荷重は552.7［N］でした。これに対し、有限要素法を使って求めたボルト変動荷重は40.97［N］とはるかに小さく、約13分の1です。

　変動荷重を有効断面積で割って、さらに2で割ると応力振幅になります。これらの数値を表4にまとめます。応力振幅が連載第2回で求めた疲労強度（A2-70 ステンレスボルトの場合：32.50［MPa］）より小さければ疲労破壊しないのですが、今回計算された応力振幅は0.34［MPa］と圧倒的に小さく、安全率は「94.34」と、疲労強度に対しては余裕をもって大丈夫ということになります。

表4　ボルト変動荷重と応力振幅の比較 ［クリックで拡大］

　有限要素法で求めたボルト変動荷重は、締め付け線図で求めたボルト変動荷重よりも驚異的に小さくなりました。どちらかが計算間違いしているのでしょうか。

締め付け線図と有限要素法の違い

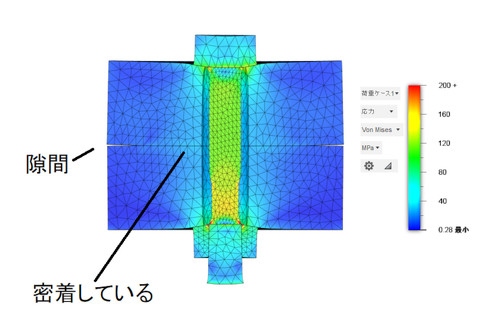
　実は、この違いは過去のねじ研究者が気付いていて、ドイツのJunker（ユンカー）博士は、内力係数に経験的に定めた係数を掛けています。また、参考文献［4］がこの問題を解決しています。参考文献［4］はちょっと難しいので筆者なりの解釈を示します。図16にミゼス相当応力図を示しますが、変形状態に注目します。被締結体同士の接触状態は、ボルトに近い側が密着しているのに対して、外周部には隙間ができています。ボルトで締結するとこのような変形をすると考えられます。締め付け線図ではこのような現象を考慮していません。

図16　ミゼス相当応力図（断面図） ［クリックで拡大］

参考文献：

• ［4］：吉本勇 他：ねじ締結体の内力係数（被締結体が中空円筒の場合）：日本機械学会論文集（1976） 第42巻 359号 P2174

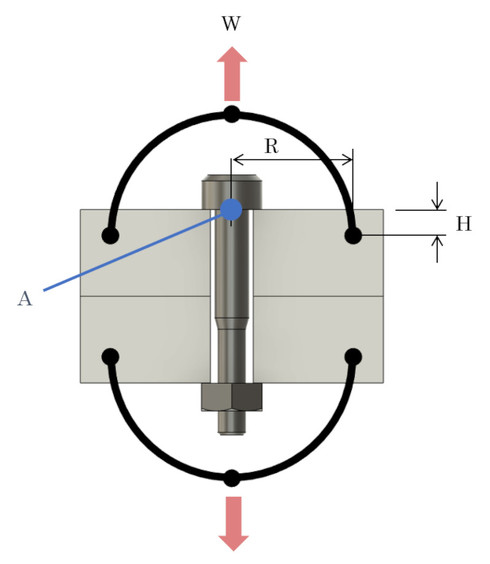
　次に、締め付け線図を作成したときの前提を図17で説明します。

図17　締め付け線図の前提 ［クリックで拡大］

　締め付け線図の検討では、ボルトと被締結体の変形は1次元モデルなので、図17においてR寸法とH寸法が0であるとして式が導かれています。つまり、力の作用点は図17のA点です。一方、図14の境界条件で示したように、荷重は被締結体の外周に作用しています。力の作用点の違いが相違の第1の理由です。A点はボルト穴の中心なので、A点に集中力が作用するような形状はないでしょう。そして、有限要素法では被締結体の変形を考慮していることが相違の第2の理由として挙げられます。有限要素法で締結体を剛体として計算すると両者は一致するでしょうが、ヤング率が無限に大きい材料もないでしょう。