車を思いのままに走らせるにはどうしたらいいの?:独学! 機械設計者のための自動制御入門(3)(4/4 ページ)
位相遅れが180度のときのゲインがマイナスだとなぜ安定なのか
そこで、車の開ループシステムの増幅率をkとすると、出力つまり車体の位置はどうなるだろうね。図10を見ながら考えてみようや
最初の半周期が過ぎてから、次の半周期に、直線道路のセンターを基準としてカーブのセンターラインの位置をk倍した、正弦波状の山のカーブを車は曲がり始める
このとき入力側のセンターラインの位置は正弦波の谷のカーブに向おうとしているよな。フィードバックシステムを構成しているから、そこに、出力側の正弦波の山のカーブが反転して加算される
……ってことは、入力には、半周期前のk倍した谷のカーブが加算されるんだ。つまり開ループシステムGoには(1+k)倍の振幅を持った正弦波の谷のカーブが入力されることになる
すると、出力には、振幅k(1+k)=k+k2の正弦波の谷のカーブが出力される。これを続けていくとどうなるか、図10を見れば分かるやろ?
そういうこっちゃ。n → ∞(無限大)とすると……
つまり、開ループシステムの伝達関数Goの周波数応答特性において、出力が入力よりも180度位相が遅れるような周波数を入力した場合、もしGoの入出力振幅比が1よりも大きければ、開ループシステムGoのループを閉じてフィードバックシステムとすると出力振幅は発散することになる。
つまりこれは不安定なシステムっちゅうことになる。だから図8のゲイン特性aの車は図7のカーブをうまく曲がれず発振してしまう
なるほど。位相遅れが180度のときの振幅比、つまりゲインが重要なんだ
さっき説明したように、ボード線図では振幅比ではなく、振幅比の常用対数の20倍を計算している。いわゆるゲインというやつだ。単位は『dB』だ。振幅比1はゲイン0dBだ
位相遅れ情報と振幅情報の2つが重要なわけだが、位相遅れを基準に考えるならば、位相遅れが180度のときのゲインが0 dBよりも大きい場合だと不安定だ。ゲインを基準に考えるならばゲインが0 dBのときの位相遅れが180度を超えていれば不安定となる
そうかぁ! そういう理屈だったのかぁ! 位相遅れが180度のときのゲインがマイナスだったらなぜ安定なのか、昔はよく分からなかったけど、いまようやく分かったよ!
位相余裕とゲイン余裕
例えば、開ループシステムのボード線図が図8のbの場合、ループを閉じてフィードバックシステムを構築すると、どうなると思う?
開ループシステムの位相遅れが180度のときのゲインは-10dBだから、振幅比kは1よりも小さい。だから安定だね?
安定は安定だけど、どのくらい安定なんだい?
そんなの分からないよ
安定性の度合いを、ゲイン0dBのときの位相遅れの大きさで見たのが位相余裕で、位相遅れ180度のときのゲインの大きさで見たのがゲイン余裕と呼ばれるものだ。図8のbの場合、位相余裕が約40度で、ゲイン余裕が約13dBだから、まぁまぁ安定だな
そうそう、これこれ。学部の授業でなんのこっちゃさっぱり分からんかったのを覚えている。そもそも安定・不安定のメカニズムを理解していなかったから当たり前といえば当たり前なんだけど。
制御の本にはサーボ機構だったら、ゲイン余裕が12から20dB、位相余裕が40から60度ぐらい、プロセス制御だったらゲイン余裕が3dB以上、位相余裕20度以上がいいと書いてあるけど、その理由がまったく分からんかった。安定・不安定のメカニズムが理解できたいまも、よく分からない
ゲイン0dBのときの位相遅れが180度を超えていれば不安定なんだから180度を基準にして、どの程度遅れが少ないかで、安定性の度合いを判断しようというのが、位相余裕だ
なるほど。位相遅れが180度のとき、ゲインが正ならば不安定で負ならば安定。だから0dBを基準としてどの程度ゲインが小さいかで安定性の度合いを判断するのがゲイン余裕だね?
でも、どうしてサーボ制御だったら、ゲイン余裕が12から20dB、位相余裕が40から60度ぐらい、プロセス制御だったらゲイン余裕が3dB以上、位相余裕20度以上がいいの?
経験値だと思っておけばいいよ
僕は経験値というのが、一番嫌いなんだよね。理屈で説明できないからなんでも経験値で逃げる。それでは技術者とはいえないんじゃないの?
よくいうな。じゃあ、理屈で説明してあげるけど、数学使うぜ?
じゃあ………………………………いいやぁ
……
参考に、図8のa、bの各ゲイン特性を有する、自動運転システムのフィードバックループを閉じたときのシミュレーションを紹介します(動画3.1)。アニメーション中にある黄色い ボールは目標位置であるセンターラインの位置を示しています。
ゲイン特性a(動画3.1)のシステムでは位相遅れが180度のときのゲインは約5dBで不安定です。発振することがシミュレーションからも分かります。ゲイン特性b(動画3.2)のシステムは発振こそしませんが、目標位置であるセンターラインにうまく追従していません。しかし制御設計では補償要素を付加することで、追従性などを改善することが可能です。補償については次回以降で解説していきます。
フーリエ変換と虹
叔父さん。実はね。さっきのフィードバックシステムにおける発振メカニズムね。あれ、ちょっと合点のいかないところがあるんだけど、聞いていいかい?
なんだい?
さっきの説明は道路のカーブが周波数ω180の正弦波の場合でしょ? そんな道路なんてめったにないから、普通の道路ならばまったく問題ないでしょ?
お前は『フーリエ変換』って知ってるか?
知ってるけど
用語
フーリエ変換とは:フーリエ変換とは、信号の時間波形から、その信号に含まれる周波数成分の強さを 求める計算方法のこと
じゃあ、直線道路を走っていても、位相が180度遅れるような開ループシステムをフィードバックすると発振する、という理由は分かるよな?
プリズムに白色光を当てると、色が分解して虹を見ることが可能です。これは光が分光されて異なる波長の光に分かれるからです。つまり白色光は波長の異なる光が集まったものであることがプリズムの分光によって分かります。
同じように、任意の信号波形についてもフーリエ変換によるスペクトル分析を行うと、波形がどのような周波数から構成されているかが分かります。つまり、信号波形もいろいろな周波数の信号が集まったものであることがフーリエ変換によるスペクトル分析によって分かるのです。
ところでわれわれの扱う電気信号には必ずホワイトノイズが乗っていることはご存じだと思います。このホワイトノイズは白色光と同じで、あらゆる周波数成分が均等に含まれていることがスペクトル分析から分かっています。従って、ノイズの中にはシステムに入力されると出力の位相が180度遅れる周波数成分が必ず存在しています。そのため、その周波数において開ループシステムのゲインが負であれば、さきほど説明したメカニズムによって、その周波数での発振現象が起きるのです。つまり、たとえ入力がなくてもシステムは発振してしまうのです。
◇
次回は、いよいよ補償による特性改善の話に入ります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 【レベル9】アセンブリ図面を作成せよ!
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 3Dモデリングツールの積層造形を支援する機能アップデート
- 【調査レポート】設計・解析業務におけるAI活用の現実と課題


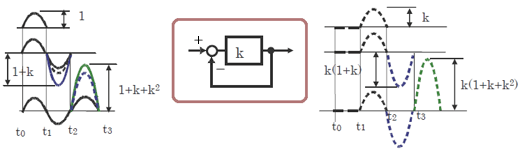 図10 発振メカニズム
図10 発振メカニズム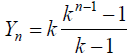

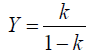
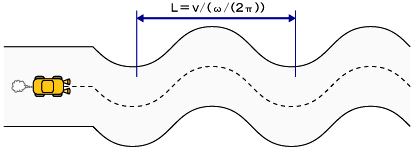 図7(再掲)
図7(再掲)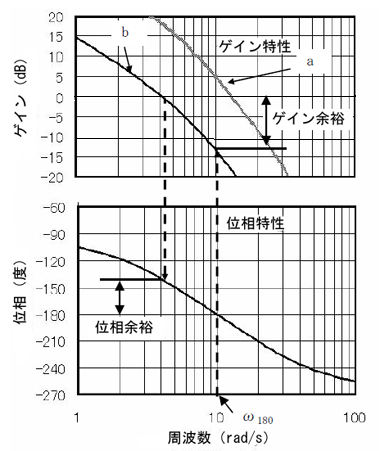 図8(再掲)
図8(再掲)









