車を思いのままに走らせるにはどうしたらいいの?:独学! 機械設計者のための自動制御入門(3)(2/4 ページ)
開ループシステムGoのループを閉じると、なぜシステムが不安定となるの?
でも、伝達関数の中身がよく分からないから、具体的なイメージがわかないな
前回の話を思い出してごらん。システムの特性は周波数応答特性によって特徴づけられるって説明したやろ。つまり伝達関数Gを周波数応答の形で表現したのが周波数応答特性でありボード線図*2だ
筆者注
*2 周波数応答特性を表現する方法としてボード線図以外にもベクトル軌跡があります。ここではボード線図に限定して話を進めますが、両者は本質的に同じものと理解してください。
ボード線図のゲイン特性における縦軸は入出力波形の振幅比の対数表示であることを思い出してごらん
ゲイン特性というのは、入力Xと出力Yの振幅比だから、まさしくG=Y/Xを意味しているんだね
ここで1つ注意しておくことがある。ゲイン特性というのは、あくまで、ある周波数の入力振幅と出力振幅の比であって、同じ時間での振幅比ではないっちゅうことや。これは図5をみれば理解できるだろ
さらに周波数応答特性には位相特性というのがあるのを思い出してほしいな。
システムの特性は、『情報や応答の遅れ』と『変化に対する過剰反応』で表現されるんだったな。『変化に対する過剰反応』というのは振幅比で、『情報や応答の遅れ』が位相差と理解すればいい。
だから『変化に対する過剰反応』についてはボード線図のゲイン特性を見ればY=G・Xで計算できる。だけど、位相についてはボード線図の位相特性からY=G・Xで計算できると思うかい?
そうだね。位相は入力からの遅れだから掛け算じゃないよね。足し算あるいは引き算だよね
そうなんだ、入力と出力の位相差は足し算、引き算だ。しかし、式(1)の表記だと出力は入力と伝達関数Gの積で計算できることになる
そうだよ。なんか変だよ
実は、複素数を使うと位相遅れもY=G・Xで計算できるんや。だけど、入出力X、Yは複素数で、その比である伝達関数Gも複素数ですっていってもイメージわかんやろ?
だから、取りあえずいまは、伝達関数Gというのは入出力の振幅比と位相差を表現するもので、その中身は周波数応答特性のことだと思ってもらえばいい
Y=G・Xの数式による具体的な計算は横に置いておいて、取りあえずここでは、その数式から導き出せるであろう周波数応答特性であるボード線図を、実験で求めたと考えればいいんだね。
そして振幅比についてはゲイン特性から普通の積のイメージで入力振幅Xから出力振幅Yが計算できる。ただし、位相については、積ではなく差として位相特性から求めることができる
そうや、そのとおりや。そこでいよいよ本題に入ろうか。開ループシステムGoのループを閉じると、なぜシステムが不安定となることがあるのか……。じゃあ、まず、開ループシステムGoを閉ループシステムにしたら、出力はどうなるか考えてみよう
ちょっと待って! 開ループシステムGoを閉ループシステムにするって、どういうこと? またまたイメージがわかないよ
何でやねん! フィードバックを構成するってことは、基本的には出力を入力と一致させるように制御するってことや。だから、図2の比較部で、目標値であるセンターラインの位置から自分の位置を引いた値、つまり偏差やね。この偏差を制御部の指令として入力するわけや
でも、偏差を制御部の指令として入力するとなぜ出力は入力に一致するの?
うん。なかなかええとこ突いてきたな。フィードバックすると出力が入力に一致するというけど、その理論的根拠は何か? ええ質問や
感心してないで教えてよー
図1の開ループシステムをフィードバックしたとすると図6のようになる
偏差εは目標入力とXと出力の差だから、
ε=X-Y3 (3)
だ。 このεが開ループ伝達関数Goの入力になるから出力Yは、
Y=Go・ε=Go・ (X-Y3) (4)
だ。
式(3)と式(4)から、フィードバックループを閉じたときの伝達関数Gcは、
Gc=Y3/X=Go/(1+Go) (5)
となるのは分かるよな?
うん、これぐらいの数式なら誰でも分かるよ。でも、式(5)を見るとGoが無限大でなければ、Gcは1とならないから、出力Yは入力Xに一致しないよね
そういうことなんや。出力が入力と完全に一致しないまでも、そこそこ同じ程度となるためには開ループの伝達関数Goは非常に大きな値である必要があるんや。しかし、Goを大きく取ると、問題が起こるんや
どんな問題が起こるの?
それが今日のテーマである、『フィードバックループを閉じるとシステムが不安定となることがある』ということなんや。それで、その理屈を図2の車の自動運転システムで具体的に説明してみようっちゅうわけや
あぁ、そういうことだったね。自動運転システムだったね。……でも目標値であるセンターラインの位置ってどうやって分かるの?
画像処理機器を使えば道路のセンターラインの位置も、車の自分の位置も分かるやろ。そういうハイテク機器を搭載していることにしようや
そうだね
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング


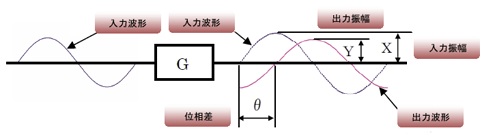 図5 周波数応答特性における入出力の関係
図5 周波数応答特性における入出力の関係

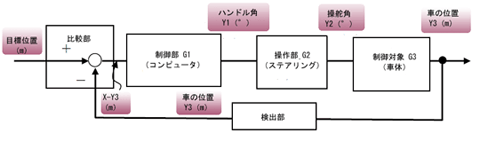 図2(再掲)
図2(再掲)
 図1(再掲)
図1(再掲)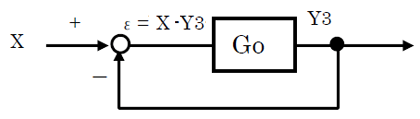 図6 閉ループシステム
図6 閉ループシステム





