CAEによる流体解析の手順を確認/実行し、紙と鉛筆による結果と比べる:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(10)(4/4 ページ)
紙と鉛筆による結果とCAE結果との比較
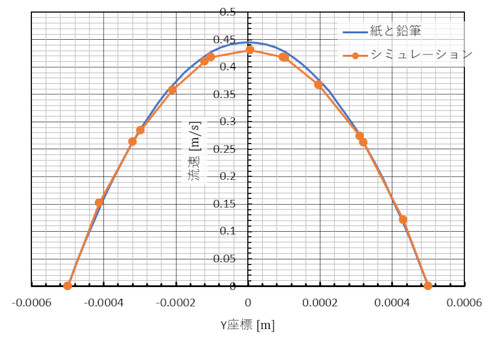
図15に軸方向流速を示します。紙と鉛筆による流速は、前回の式21によるものです。紙と鉛筆による結果と、CAE解析の結果は非常によく一致しました。層流においては、理論値とシミュレーション結果を一致させることは、案外難しくありません。
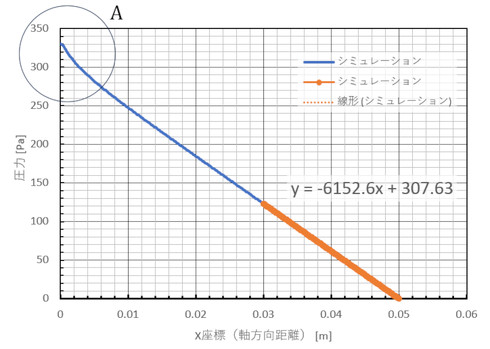
図16に圧力分布を示します。A部が直線でありません。助走区間において、圧力損失が大きくなっていることが分かります。
図16のオレンジ色のグラフの傾きが圧力勾配を示しており、グラフから読み取ると−6513[Pa/m]となりました。紙と鉛筆による圧力勾配は、前回の式23から求めることができ、式4となります。数値を代入すると、−6331[Pa/m]となり、圧力損失も非常によく一致していることが確認できました。
何だか、紙と鉛筆による計算とCAE解析の結果を一致させることが目的のように見えるかもしれませんが、本来の目的は、冷却系の設計計算Excelシートを作成することと、シミュレーション手順を紹介することにあります。紙と鉛筆による計算と、CAE解析の結果を比較し、その一致を確認することで、Excelシートとシミュレーション手順の正しさを相互に確認することができました。
次回は、有限体積法の手順を説明します。通常、気体の流体解析はマッハ数が0.3[-]以下であれば、非圧縮流体として取り扱って差し支えありません。ですが、マッハ数が0.003[-]という圧縮流体の実験値を持ち合わせていますので、層流の圧縮流体の圧力損失を求めて、その結果を実験値と比較してみたいと思います。 (次回へ続く)
参考文献:
- [1]生井武文、井上雅弘|機械工学基礎講座 粘性流体の力学|理工学社(1978)
- [2]日本機械学会|機械工学便覧 A5 流体工学|(1992)
Profile
高橋 良一(たかはし りょういち)
RTデザインラボ 代表
1961年生まれ。技術士(機械部門)、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。
構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置(MRI装置)の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在RTデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ RTデザインラボ
関連記事
 時々刻々と変化する温度分布
時々刻々と変化する温度分布
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第8回は、非定常熱伝導問題に取り組む。 「ふく射」による熱の伝わり
「ふく射」による熱の伝わり
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第7回は、「ふく射」による熱の伝わりについて考える。 CAEソフトに仕掛けられたトラップ
CAEソフトに仕掛けられたトラップ
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。第1回のテーマは「CAEソフトに仕掛けられたトラップ」だ。 連載「CAEを正しく使い疲労強度計算と有機的につなげる」の内容と有限要素法
連載「CAEを正しく使い疲労強度計算と有機的につなげる」の内容と有限要素法
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第2回では本連載の「あらすじ」と「有限要素法」について取り上げる。 解析専任者に連絡する前に、設計者がやるべきこと
解析専任者に連絡する前に、設計者がやるべきこと
連載「CAEと計測技術を使った振動・騒音対策」では、“解析専任者に連絡する前に、設計者がやるべきこと”を主眼に、CAEと計測技術を用いた機械の振動対策と騒音対策の考え方や、その手順について詳しく解説する。連載第1回では、本連載の趣旨、振動対策や騒音対策が必要となる場面などについて取り上げる。 設計者なら一度はやってみたい形状最適化、お金をかけずにどこまでできる?
設計者なら一度はやってみたい形状最適化、お金をかけずにどこまでできる?
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

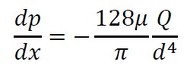 式4
式4






