CAEによる流体解析の手順を確認／実行し、紙と鉛筆による結果と比べる：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（10）（3/4 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

手順5：計算

　これで、セットアップが完了しました。データを保存して計算を実行します。有限体積法では繰り返し計算で解を求めるため、少し時間がかかります。

手順6：結果の表示

　計算結果を読み込んで、いろいろなパラメーターを表示します。有限要素法による弾性解析では、物体の表面の応力や変位を表示しました。これに対し、流体解析の流体領域の表面の流速はゼロか、境界条件の値であり、見ても仕方ありません。そのため、平面を定義して、その平面で切った断面の速度などを見ることになります。

　等高線表示（コンター図）で可視化できる量としては、速度、圧力、温度、そしてy＋（こちらはいずれ説明します）などがあります。ベクトル表示では、主に速度ベクトルが表示対象となります。また、流体解析では流線を表示します。流線については、出発面を指定することが可能で、普通は入り口となります。

　なお、シミュレーション結果をテキストファイルとして出力する手順については、使用しているCAE解析ソフトのサポート窓口に確認しておくことをオススメします。筆者の流儀として、解析結果をテキストファイルで出力することは、固体解析でも流体解析でも欠かせません。

　以上が、流体解析の手順となります。

円管層流のシミュレーション

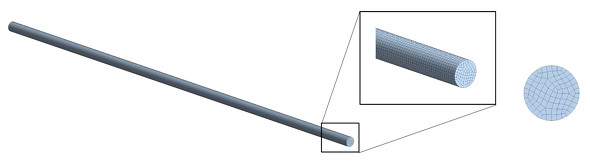
　いよいよシミュレーションの実行です。今回は、直径1［mm］の円管内を流れる層流を対象に計算しましょう。図10に、セル分割図を示します。層流の場合、セル分割の細かさは、“見たいところを細かくする”程度の配慮で十分です。一方、乱流のセル分割の場合は異なる配慮が必要となりますが、この点についてはいずれ説明します。

図10　円管層流のセル分割図［クリックで拡大］

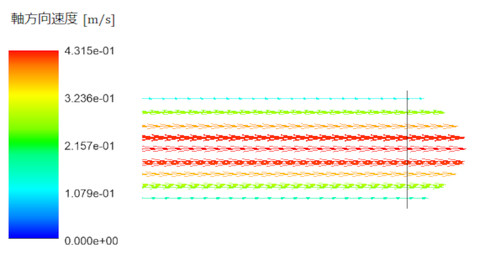
　図11に出口近傍における速度ベクトルを示します。また、図12には軸方向の速度分布を示しています。

図11　速度ベクトル［クリックで拡大］

図12　軸方向速度分布［クリックで拡大］

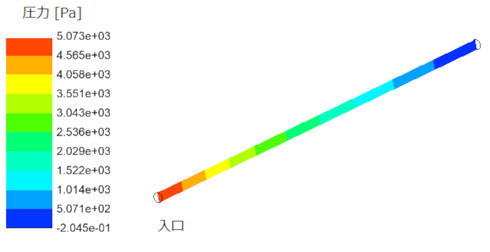
　図13に圧力分布を示します。

図13　圧力分布［クリックで拡大］

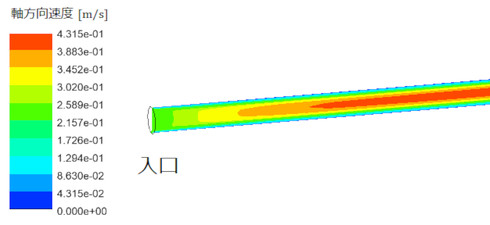
　ここで、「ちょっと待った！」と言いたくなるかもしれません。圧力の低下の度合いが、等ピッチではありません。前回、「圧力勾配は一定値だ」と説明しました。違いを確認するために、入り口近傍の速度分布を調べましょう。図14に示します。

図14　入り口近傍の軸方向流速分布［クリックで拡大］

　今回は、入り口の境界条件として、入り口断面における速度を一様としました。これは、大きなタンクに細い管をつないだ状態をイメージしたものです。このような入り口近傍の一様な流れが、放物線状の層流へと変化するまでの区間のことを「助走区間」と呼びます。

　助走区間の長さは、式3で求めることができます（参考文献［2］）。数値を代入すると、その長さは14［mm］となります。管の直径が1［mm］なので、図14を見る限り、助走区間の長さとしては妥当な範囲のようです。

式3