圧縮性流体の圧力損失を求めて実験値と比較する：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（11）（1/5 ページ）

CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第11では、マッハ数が0.003［-］という実験値を基に、層流における圧縮流体の圧力損失を求め、その結果を実験値と比較する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　前回、流体シミュレーションの例を紹介しました。通常、圧縮性流体（気体のことです）の解析では、マッハ数が0.3［-］以下のときは非圧縮流体として取り扱って構いません。

　今回は、マッハ数が0.003［-］での圧縮流体の実験値を持ち合わせているので、この条件で層流における圧縮流体の圧力損失を求めてみましょう。

⇒「連載バックナンバー」はこちら

圧縮性流体の圧力損失

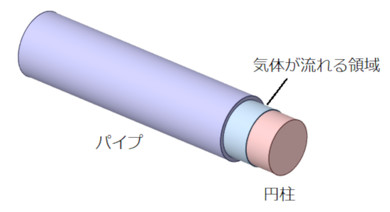
　パイプと同軸に円柱がセットされていて、そのパイプと円柱の隙間に気体が流れる問題を検討してみましょう。図1のような感じです。

図1　気体が流れる領域［クリックで拡大］

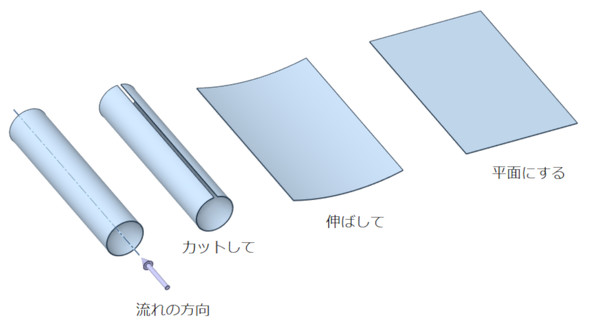
　この気体が流れる領域は非常に薄いため、近似として図2に示すように、流れる領域を平面に変形して扱います。

図2　気体が流れる領域の変形［クリックで拡大］

　これによって、流れを2次元問題として取り扱うことができるようになりました。

平行壁間の流れ

　圧縮流体の計算に入る前に、図2の平面にした状態の流れを求めましょう。

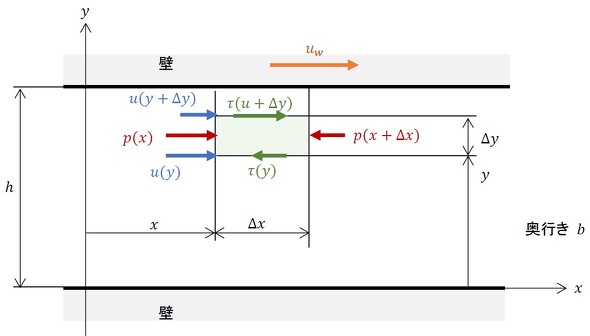
　図3に解析モデルを示します。

図3　平行壁間流れの解析モデル［クリックで拡大］

　この問題は「平行壁間の流れ」といいます。上下に壁があり、その間に流体が流れています。ここでは、上側の壁が速度u_wで動いているケースを扱います。

　流体内の、長さΔx、高さΔy、奥行きbの小さな直方体を考えます。流速uはy座標だけの関数、圧力pはx座標だけの関数とし、uとpは奥行き方向に一定値であると考えます。

　y＝yの位置での流速はu（y）、せん断力はτ（y）、y＝y＋Δyの位置での流速はu（y＋Δy）、せん断力はτ（y＋Δy）です。x＝xの位置での圧力はp（x）、x＝x＋Δxの位置での圧力はp（x＋Δx）になります。

　せん断応力の向きについてですが、直方体の下辺では、下側の流体が直方体の動きを引き留めているため、マイナス方向に働きます。一方、直方体の上辺では、上側の壁が速度u_wで動いており、上側の流体が直方体を引っ張るため、プラス方向になります。