圧縮性流体の圧力損失を求めて実験値と比較する:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(11)(4/5 ページ)
» 2025年07月16日 07時00分 公開
[高橋良一/RTデザインラボ 代表,MONOist]
圧縮流体の圧力損失
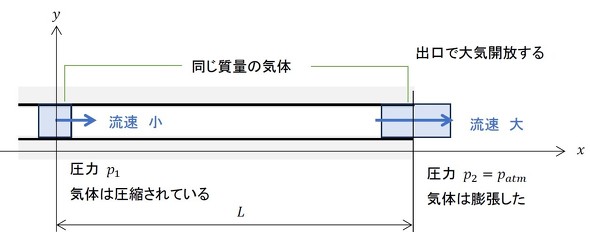
準備が整ったところで、圧縮流体の圧力損失を求めていきましょう。図1のような場合は圧力損失が大きく、上流と下流で圧力差があるため、流速にも変化が生じます。これまでは「流速は流れ方向に一定」と仮定していましたが、この仮定は適用できなくなりました。
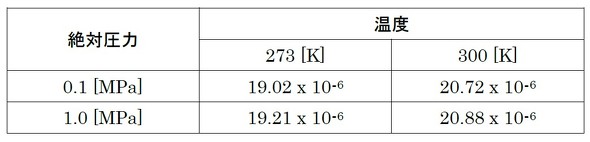
またしても積分が登場します。そこでまず、気体の粘性係数が圧力によってどのように変化するかを確認しておきましょう。表1に、酸素の粘性係数データを示します。温度によって粘性係数は変化しますが、絶対圧力が10倍になっても、粘性係数はほとんど変化していません。これはラッキーです。積分の際、粘性係数を定数として扱って問題なさそうです。
ここでの気体は酸素です。酸素を理想ガスと見なすと、式19が成立します。
これを変形します(式20)。
今、断面積A[m2]の流路内において、ある位置の圧力をp[Pa]、平均流速をum[m/s]、気体の密度をρ[kg/m3]とします。出口は大気開放されており、出口の圧力はpatm、平均流速はuatm、密度はρatmです。流路のどの位置でも質量流量は等しいため、式21が成立します。
1[kg]当たりの体積vは、密度ρの逆数なので、ρ=1/vです。これを式21に代入し、変形します(式22)。
続いて、式22に式20を代入します。
ここで、平均流速の式を使います(式24)。
式24に式23を代入し、変形します(式25)。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
Special SitePR
あなたにおすすめの記事PR

 式19
式19 式20
式20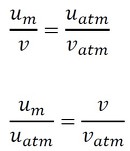 式22
式22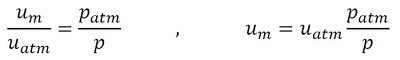 式23
式23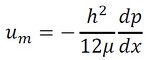 式24
式24 式25
式25





