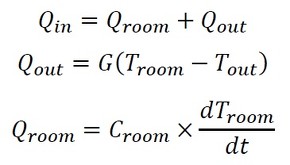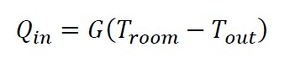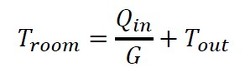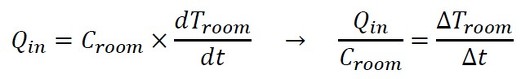何のためのモデリング？　～1Dモデリングの目的を原点に立ち返って考える～：1Dモデリングの勘所（41）（1/5 ページ）

「1Dモデリング」に関する連載。連載第41回では原点に立ち返り、モデリングを実施する目的からスタートし、現象の理解、あたり評価、モデリング、解析、評価に至るまでの一連の流れを2つの事例を通して考える。

» 2025年03月19日 06時00分 公開

　これまで40回にわたって「1Dモデリング」とは何か、モデリングの種類、方法を主に分野別に紹介してきた。モデリングを行うことは、それ自体意味のあることだが、本来は何かの目的のために実施するものといえる。その目的の主たるものが設計であり、このための対象とする現象の理解と表現である。

　一方、実際の設計においては、こちらの専門とは関係なく解を求めることが要求される。すなわち、現象を見て、それが何に起因するものなのかを類推、表現することが求められる。

　このような背景の下、本連載では、設計（主に機械設計）を行う上で遭遇すると思われるさまざまな現象を取り上げ、そのモデリング方法について考えてきた。今回は視点を変えて目的からスタートし、現象の理解、中り（あたり）評価、モデリング、解析、評価に至るまでの一連の流れを2つの事例を通して考えてみたい。

⇒連載バックナンバーはこちら

住宅環境を省エネ視点で考える

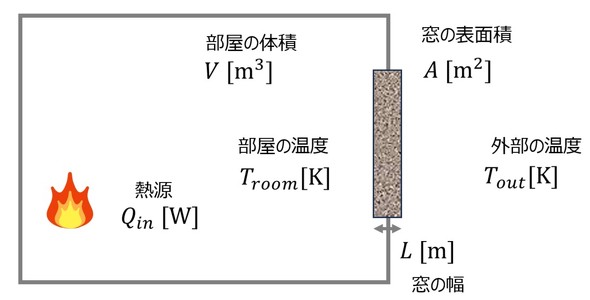
　身近な例として、住宅環境における暖房を省エネ視点で考えてみたい。図1に示す集合住宅のある部屋を考える。部屋にはQin［W］なる熱源があり、面積A［m2］、幅L［m］の窓を介して外気と接している。部屋の体積はV［m3］とし、窓以外は外部とは断熱されているものと考える。

　ここで知りたいこと（目的）は、窓の種類がどのように影響するのか、外気の影響（ここでは、外気温Tout［K］は一定として、風速の影響）がどの程度なのかとする。

集合住宅のある部屋 図1　集合住宅のある部屋［クリックで拡大］

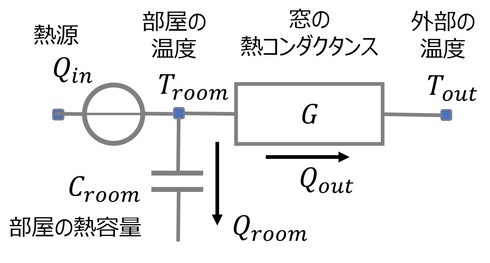
　伝熱現象のモデリング方法は連載第31回と第32回で既に紹介している。その方法を用いて図1をモデル化すると、図2となる。

集合住宅のある部屋の伝熱モデル 図2　集合住宅のある部屋の伝熱モデル［クリックで拡大］

　図2を式で表現すると以下となる。

　Qroom［W］は部屋に蓄えられる熱量、Qout［W］は外に逃げていく熱量、Troom［K］は部屋の温度、Croom［J/K］は部屋の熱容量、G［W/K］は窓の熱コンダクタンスである。上記の式をいきなり解いてもよいが、まずは大まかな傾向を見るために、定常状態を考える。定常状態ではQroom＝0となるので、Qin＝Qoutとなり、

　これより、

となる。すなわち、窓の熱コンダクタンスが良いと（断熱性能が悪いと）、部屋の温度は果てしなく外気温に近づいていく。また、窓が断熱状態だと（G＝0）、少しの入熱量でも理論上、最終的に部屋の温度は∞になる。

　一方、部屋が完全に断熱されていると、（G＝0，Qout＝0）、Qin＝Qroomとなるので、非定常の式から、

となり、室温をある温度にするために必要な熱量または時間を知ることができる。

　以上のように、モデリングとは導出した式を数値的に解いて結果を知るだけでなく、式の意味を理解することにより、解かなくても（解く以前に）多くのことを知ることができる。

　　　　　　 1|2|3|4|5 次のページへ

Copyright © ITmedia, Inc. All Rights Reserved.