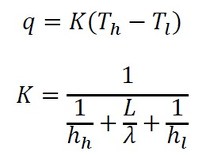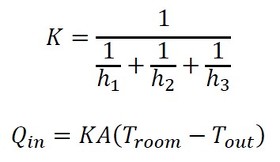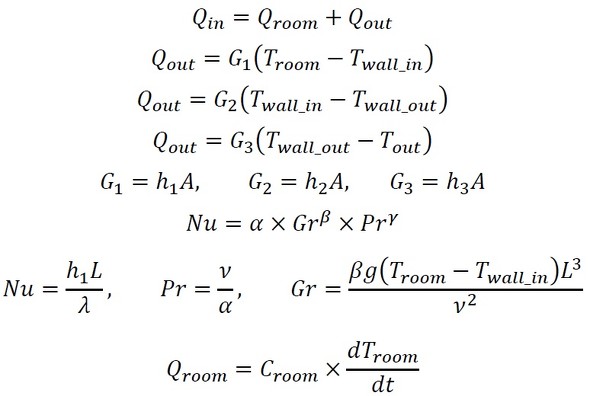何のためのモデリング？ ～1Dモデリングの目的を原点に立ち返って考える～：1Dモデリングの勘所（41）（2/5 ページ）

[大富浩一／日本機械学会 設計研究会，MONOist]

印刷する

通知する 連載「％」の新着をメールで通知

鬯ｯ�ｯ�ｽ�ｯ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｮ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｫ鬯ｯ�ｯ�ｽ�ｯ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｩ鬯ｮ�ｯ陷茨ｽｷ�ｽ�ｽ�ｽ�ｹ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｨ鬯ｯ�ｯ�ｽ�ｩ髯晢ｽｷ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｧ鬯ｯ�ｮ�ｽ�ｫ�ｽ�ｽ�ｽ�ｰ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬩包ｽｶ闕ｵ證ｦ�ｽ�ｩ�ｽ�ｸ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｹ鬯ｯ�ｯ�ｽ�ｯ�ｽ�ｽ�ｽ�ｮ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｫ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｴ鬯ｯ�ｯ�ｽ�ｮ�ｽ�ｽ�ｽ�ｮ鬮ｫ�ｲ陝ｷ�｢�ｽ�ｽ�ｽ�ｶ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｣�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽPost

Shareシェア

-はてなブックマーク

　次に、窓の熱コンダクタンスについて考える。窓の熱コンダクタンスは連載第21回で紹介した通り、図3のように表現できる。

図3　窓の熱コンダクタンス［クリックで拡大］

　図3を式で表現すると、

となる。q［W/m²］は熱流束、K［W/m²・K］は熱通過率でG＝KAの関係がある。また、h_h［W/m²・K］は高温側の熱伝達率、h_l［W/m²・K］は低温側の熱伝達率、λ［W/m・K］は熱伝導率である。

　一方、窓構造は複雑であり、業界では「熱貫流率」（次元は熱伝達率に等しい）という値を用いて定義されているため、ここではその値を用いることにする（参考文献［1］）。これにより、窓の熱コンダクタンス（熱通過率）は、高温側の熱伝達率をh₁、窓の熱貫流率をh₂、高温側の熱伝達率をh₃とすると以下のように表現できる。

　熱伝達率は、連載第32回で述べた方法で算出できる。高温側（室内側）は自然対流熱伝達とし、室温と窓表面の温度差は15℃とする。低温側（室外側）に関しては、無風状態の場合は自然対流熱伝達とし、外気温と窓表面の温度差は15℃に、風がある場合は強制対流熱伝達として計算する。一方、窓の熱貫流率（窓表面と空気との熱伝達は含まれない）は、文献の情報を整理して、

［クリックで拡大］

の値を用いることにする。

　以上の情報を用い、3種類の窓（1枚ガラス、複層ガラス、真空ガラス）について、外気温10℃で室内温度を25℃に保つために必要な熱量を求めると表1となる。なお、外気の状態は無風／中風／強風の3段階を考えた。

表1　窓ガラスの種類と必要熱量の関係［クリックで拡大］

　表1から、窓を1枚ガラスから複層ガラスまたは真空ガラスに取り換えることで必要熱量が半分程度になり、省エネに効果があることが分かる。このように、式を数値的に解く以前に結果の中りを付けることを、中り評価または中り計算という。

　ここまでの検討で知りたいことの大半は分かった。ただ、実際には窓ガラス表面の自然対流は、窓ガラス表面温度が関係している。以上の検討ではこれを無視していた。そこで、最後に確認の意味も含めて詳細なモデルを作成し、中り評価の妥当性を確認することにする。

　詳細伝熱モデルは図4となる。

図4　集合住宅のある部屋の詳細伝熱モデル［クリックで拡大］

　図4を定式化すると以下になる。ここでは自然対流の式も考慮している（詳細は連載第32回を参照のこと）。

　計算では、図5に示す諸元を用いる。

図5　解析上の諸元［クリックで拡大］

参考文献：

• ［1］二重窓の熱貫流率について｜日本サッシ協会（2020）

印刷

通知 連載「％」の新着をメールで通知

鬯ｯ�ｯ�ｽ�ｯ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｮ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｫ鬯ｯ�ｯ�ｽ�ｯ�ｽ�ｽ�ｽ�ｯ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｩ鬯ｮ�ｯ陷茨ｽｷ�ｽ�ｽ�ｽ�ｹ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｨ鬯ｯ�ｯ�ｽ�ｩ髯晢ｽｷ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｧ鬯ｯ�ｮ�ｽ�ｫ�ｽ�ｽ�ｽ�ｰ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬩包ｽｶ闕ｵ證ｦ�ｽ�ｩ�ｽ�ｸ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｹ鬯ｯ�ｯ�ｽ�ｯ�ｽ�ｽ�ｽ�ｮ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｫ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｴ鬯ｯ�ｯ�ｽ�ｮ�ｽ�ｽ�ｽ�ｮ鬮ｫ�ｲ陝ｷ�｢�ｽ�ｽ�ｽ�ｶ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｣�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽPost

Shareシェア

-はてなブックマーク

SharePocket Button