ターボ機器の流体解析と最適化設計:実務経験者が教える! ターボ機器の設計解析の勘所(6)(4/4 ページ)
2-5 多目的最適化
一般には、実務上の設計問題は複数の目的を持つ多目的最適化問題です。さまざまな要求から、できる限り多くの性能項目を高めて、機器を利用するユーザーの要望に応えようとします。しかし、多目的の最適化は、互いに相反する傾向がある、すなわちトレードオフの関係にある場合が多いです。例えば、ファンを設計するときの効率と静圧上昇(圧縮機の圧力比)、ポンプを設計するときの小型化とキャビテーション性能、など現実の設計でも非常に難しい問題だと筆者は思います。
相反する複数の目的関数は図6.6のようなパレート解の形で表されます。最適化問題における拘束条件の範囲では、この図のようにある一定の曲線を限界として、CFD解析の結果が並ぶ形になります。この曲線を「パレートフロント」、パレートフロント上に並ぶポイントを「パレート解」と呼びます。パレート解は、「より優れた解が存在しない解の集合」といえます。パレート解同士の優劣は基本的にはありませんが、設計者が設計思想に応じて複数のパレート解から、より意図に合う組み合わせを選ぶことになります。
2-6 ロバスト最適化
最適化設計を行って得られた設計変数の組み合わせを適用して、実際にターボ機械を製作するのですが、実際に製作する羽根や流路の形状を設計寸法に完全に合わせて製作することは不可能であり、必ず何らかの寸法誤差が伴います。
一般的に、性能向上を追求していくと、寸法誤差があった場合に、形状の違いにより性能が狙った水準から下がってしまう場合があります。製作する機器ができる限り確実に所望の性能を出すためには、形状が多少変わっても性能が下がらない、安定性の高いロバストな解を求める必要があります。従って実設計で最適化を行う場合は、設計パラメータの微小変動を考慮したロバスト最適化(参考文献[10])が重要な課題となります。
3. できるだけ効率的に最適化設計を行いたい
形状寸法を設計変数として最適化設計を行った場合は、CFD解析を行うモデルの形状をどのように変更するかによって、最適化システムの構築に要する手間も異なってきます。また1回のCFD解析を行うために必要なソフトウェア実行が少ないほど、最適解を求めるのに要する時間が短くて済みます。通常は、形状ごとにCADで形状を生成して、解析メッシュを生成し、計算条件を設定してソルバ実行、というプロセスを実行します。しかし、解析メッシュ生成までの過程は、ツールの使い方次第で大きく効率を上げることが可能です。以下で、その手法をいくつか紹介します。
3-1 自動メッシュ生成システムを利用する
解析メッシュを作る場合は、CADデータを読み込み、その形状をベースにメッシュ生成を行うことが多いと思います。最適化システムのワークフローでメッシュ生成を行う際は、メッシュ生成ソフトウェアで、対象形状の定義を行い、表面メッシュ、体積メッシュを生成するまでの過程を自動的に行うスクリプトを作成すれば、CADデータを用いることなくCFD解析を行って、性能を求める対象としたい形状に解析メッシュを生成することができます。
形状最適化における形状変更の際、メッシュ生成ソフトウェアを利用するメリットは、多少大きな変形をしても、CFD解析で十分結果が得られるだけのメッシュ品質を確保できることだと思います。壁面付近に生成する、境界層メッシュのサイズを厳密に管理する場合なども同様です。
3-2 メッシュモーフィング
「メッシュモーフィング」とは解析メッシュ形状を直接変形させる技術です。「モーフィング」とはコンピュータグラフィックスの世界で、画像を徐々に変化させる数値的技術のことを指します。この考え方を解析メッシュの変形に応用したものがメッシュモーフィングです。ボリュームメッシュまですべて一度に、解析メッシュデータを直接モーフィングすることにより、計算条件の再設定やリメッシュ(メッシュの切り直し)なくCFD解析を実行できます。
図6.9にメッシュモーフィング技術の一例を示します。
既存のメッシュモデルの変形対象部位を囲うように変形制御するための制御点で構成されるボリュームを設定して、制御点移動により簡単にモーフィングできます。またリメッシュしない限りは、メッシュモーフィングの前後で格子節点の数や節点番号は変わりませんので、形状変形ごとのCFD解析精度のばらつきは少なくなります。つまり、解析結果として得られた性能の変化は、どのメッシュが粗く、どのメッシュが細かいかといったメッシュの切り方の影響がなく、ほぼ形状変更のみによるものといえます。すなわち最適化設計自体も高い精度が得られているといえます。
この技術によって、形状最適化を行う際に、初期モデルさえ作っておけばCADモデル生成とメッシュ生成のプロセスを構築せずに最適化ワークフローを組むことができますので、非常に効率的に最適化設計を行うことができます。
3-3 3次元逆解法設計
本連載の第2回で触れましたとおり、羽根負荷分布を規定してそれを満たす羽根形状を求める3次元逆解法が実用化され、ターボ機械の開発に活用されています。
応用数理学を始めとするさまざまな分野に「順問題」と「逆問題」という言葉があります。原因から結果を推論して解く問題を順問題、逆に結果から原因を推論して解く問題を逆問題といいます。ターボ機械では、「結果」は運転したときの流れ場や性能特性を指し、「原因」はターボ機械の流路や羽根形状を指します。優れた性能が得られる流路・羽根の形状を決めるのがターボ機械の設計ですから、そもそもデザインというのは逆問題であることが分かると思います。
ただ逆問題を解くことは一般的には非常に難しいことです。このため設計検討の過程では、いったん設計した形状でどのような性能が得られるか、実験やCFDを使って求める順問題を繰り返して設計と性能の関係を求めます。これに対して理想的な流れ場の条件を規定して、それを実現する形状を求める逆問題をコンピュータで解析して求めるのが「逆解法」です。
ザンゲネ(Zangeneh)の提唱する3次元逆解法(参考文献[11][12])は、非粘性・非回転であるポテンシャル流れの仮定の下で周方向に平均した旋回速度を使って表現される強さの渦層によってターボ機械の翼面を表現します。翼負荷分布は次式で表されます。
この3次元逆解法と最適化システムを組み合わせることにより、効率的に最適化設計を実施することができます。最も大きなメリットは、流体力学的に性能への影響が大きいと考えられる変数を設計パラメータとして選定できることや、羽根曲面などパラメータで規定しにくい設計変数を少ないパラメータで表現できることではないでしょうか。図6.10に3次元逆解法設計を用いた最適化システム(参考文献[13])の流れを示します。
4. 設計は、コンピュータ上だけで終わらない
6回にわたりお付き合いいただきました連載も、今回で最終回となります。
「実務経験者が教える ターボ機器設計解析の勘所」と題しまして、ターボ機械設計、流体解析設計、最適化設計とできるだけ分かりやすく説明させていただいたつもりですが、いかがでしたでしょうか。
ターボ機械や流体解析に限らず、CAE(Computer Aided Engineering)を利用した設計は、現在、幅広い産業分野で利用されています。
今回の連載を通じて一番お伝えしたかったことは、数式や解析やシミュレーションでターボ機械が設計されるとはいえ、設計しているものはコンピュータのモニタ上で完成するものではなく、あくまで実際の機械であるということ――材料を削ったり溶かしたり、部品を組み立てたりして、出来上がる機械であるということです。そのためにはその実際の機械の動きや空気の流れを想像し、人が使うことを思い浮かべながら設計することが大切です。流体解析の結果でモニタに赤く表示される「1000Kの空気」の熱気をぜひ想像しながら感じてください。
このシリーズが少しでも皆さまのお役に立てれば幸いです。改めまして、ご愛読ありがとうございました。
本記事の参考文献リスト
◎併せて読みたい「CAE」関連ホワイトペーパー:
» 横浜ゴムのタイヤ開発を推進する“AI×CAE×ヒト”による三重奏
» 設計者が実施すべき解析“3つ”のポイントと最新CAE技術動向
関連記事
 設計者CAEとは何なのか
設計者CAEとは何なのか
機械メーカーで3次元CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は設計者CAEについて考える。 材力とFEMをシッカリ理解して、シッカリ解析!
材力とFEMをシッカリ理解して、シッカリ解析!
小難しい有限要素法を数式を使わずに解説する。まずは有限要素法の歴史を振り返り、解析の基本的な考え方を確認。 CAEは高度化と簡易化に分かれる、生産技術CAEも充実
CAEは高度化と簡易化に分かれる、生産技術CAEも充実
「第26回 設計・製造ソリューション展(DMS2015)」では、VDI環境でのCAE実施や、高度な解析が社内でも使えるようになるなど、一層CAEの利用範囲の拡大が感じられた。 設計者CAEについて、また考え始めよう
設計者CAEについて、また考え始めよう
2017年はCAE関連企業の買収が進み、設計者CAEというキーワードが再び注目されだしている。2018年も設計者CAE関連の技術の進化に注目していきたい。 「ないと困るなら、復活させればいい」――本当に役に立つCAEの導入方法とは
「ないと困るなら、復活させればいい」――本当に役に立つCAEの導入方法とは
CAEの導入効果は意識して示さなければ外部から見えにくい面もある。またともすればツールの導入ばかりに力が入ってしまい、効果の検証が後回しになってしまうこともある。その問題を解決しようと、いったんCAEの専門組織を凍結してしまうという荒療治を行ったのがオムロンだ。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
 図6.6 パレート解とパレートフロント
図6.6 パレート解とパレートフロント 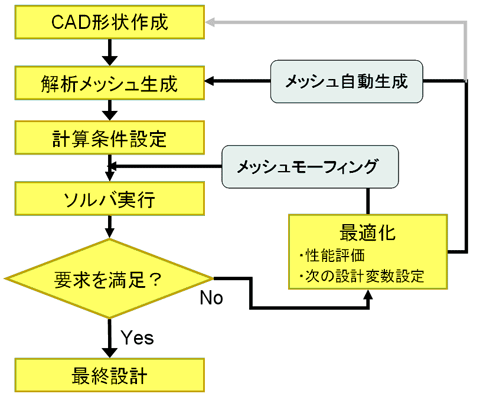 図6.7 最適化システムにおけるメッシュ自動生成とメッシュモーフィングの位置付け
図6.7 最適化システムにおけるメッシュ自動生成とメッシュモーフィングの位置付け 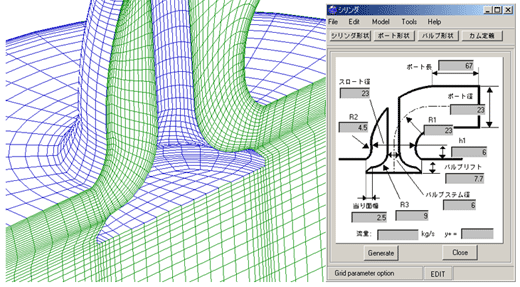 図6.8 自動メッシュ生成システムの一例
図6.8 自動メッシュ生成システムの一例 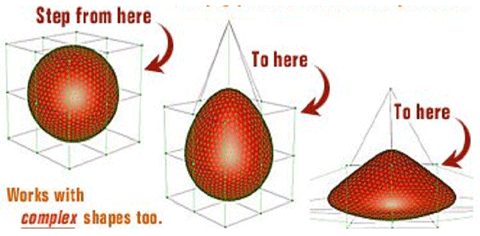 図6.9 メッシュモーフィング技術の一例
図6.9 メッシュモーフィング技術の一例 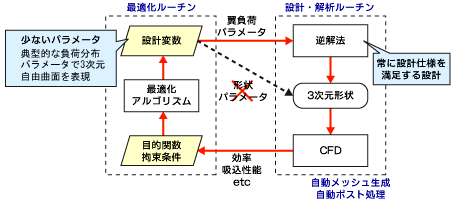 図6.10 逆解法設計を活用した最適化設計フロー
図6.10 逆解法設計を活用した最適化設計フロー 





