ターボ機器の流体解析と最適化設計:実務経験者が教える! ターボ機器の設計解析の勘所(6)(1/4 ページ)
最終回は、これまで説明してきた流体解析を利用したターボ機械の「最適化設計」について解説する
これまでの連載では、ターボ機械を設計し、出来上がった形状に関してコンピュータを使ってシミュレーションを行って性能を求め、羽根車内の流れがどのようになるかを確認するまでの過程を説明しました。
今回は最終回として、これまで説明してきた流体解析を利用した「最適化設計」を紹介します。コンピュータを使い、「ターボ機械を設計するための変数を種々に修正しながら性能を向上する」というプロセスを自動的に行います。
1. 最適化設計とは?
まず、「最適化設計とは何か」について簡単に説明しましょう。
「最適(Optimum)」とは「最も適していること」を示す言葉です。「最適化」とは、「最適である」として求められた解、つまり最適解を求めることです。
最適化を取り扱う問題を「最適化問題」といいます。
例えば、
- 小豆「x」kg・米「y」kg・砂糖「z」kgでおはぎとかしわもちを作って売る場合、売り上げが最大になるにはそれぞれ何個ずつ作る?
- 何カ所かを訪問するタスクがあって、それぞれの地点間を移動する時間とコストが分かっているような場合、最も少ない時間とコストで移動するにはどの順番で回ればよいか?
など、世の中にはいろいろな最適化問題が存在します(参考文献[1][2][3])。
できる限り効率よく、かつ少ない労力で、複雑な最適化問題を解くために、取り扱う問題は数学的な関係として定式化されます。一般に、目標と変数、その両者の関係である目的関数、および各変数の制約条件(規定範囲)の関係で表される場合が多いです。この条件下で、目的関数の値が、最大になるか、最小になるか、あるいは「特定の値」になるか? ……のいずれかの形で変数を求めることになります。
この最適化問題を機器設計に適用して、与えられた範囲(制約条件)の下で、性能(目的関数)を最も優れたものにする設計パラメータを数理的に求めるのが「最適化設計」です。
本連載の第1〜2回で説明したように、ターボ機械の設計では、設計仕様を満足することができるような運転条件と流路形状・羽根形状を規定します。図6.1のフローに示すとおり、最終設計を得るまでの過程で、設計者は経験や勘に頼って設計パラメータを決定し、試行錯誤を重ねて設計と評価をすることが多いと思います。
本連載の第3、4、5回で説明した流体解析(CFD:Computational Fluid Dynamics)と最適化設計を組み合わせると、設計プロセスは図6.2に示す形になって、試行錯誤を経て最終設計を求めるプロセスを完全に自動化することができますので、非常に効率よく設計を行うことできます。
また最適化の過程で、設計と性能の関係がより詳細に明らかになるので、これまでにない高い性能を得られることが期待できます。
2. どのような手順で「最適化設計」を実施するか?
2-1 設計変数、目的関数を決める
先ほど説明したように、与えられた範囲(制約条件)の下で、性能(目的関数)を最も優れたものにする設計パラメータを求めるのが最適化設計です。最適化設計の始めに、設計変数として何を変化させ、性能としてどのような項目を選び、どのような結果を求めるかを決めなければなりません。設計変数をあまり多く選び過ぎると、設計変数と性能の関係である「目的関数を求めるためのプロセス」が非常に複雑となり、設計結果を求めるまでに多大な時間が必要となってしまいます。そのため、性能向上に効くパラメータを確実に選択することが、最適化設計を実施するうえで非常に重要です。また、目的関数となる性能も、CFDによって高い精度で求められる物理量であることが必要です。
では、ターボ機械の場合は、この最適化設計をどのように適用できるでしょうか? 例えば、羽根車設計に当てはめてみましょう。
羽根車設計では、1次元設計と3次元設計を経て、流量、揚程、回転数、子午面形状、羽根形状が、それぞれ決定されます。現在の計算機技術では、ターボ機械全体の流路をモデル化してCFD解析を実行できますので、実際に運転して計測される性能項目は、ある程度の精度で求めることができます。設計で決められるパラメータのうち、流量・揚程は要求仕様として規定され、回転数は強度上の限度から最適化設計のパラメータに選定されることは、ごく少ないと考えられます。そのため、ターボ機械の最適化設計は、目的となる性能を最も優れたものにするための形状を決定する設計問題、すなわち形状最適化問題といえます。子午面形状を決定するための入口径や出口径、あるいはハブ形状など、羽根形状が設計変数になる場合は、出入口羽根角度や羽根角度分布における曲率や、最大および最小角度を持つ位置、などが変数として考えられます。
ターボ機械の最適化設計で、目的関数として選定される性能項目の例を下の表6.1に示します。ここで、目的関数として選定される性能は1つだけとは限りません。このように複数の目的関数を持つ最適化設計を「多目的最適化」と呼びます。多目的最適化において、どのように問題が複雑化するかについては、後ほど説明します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
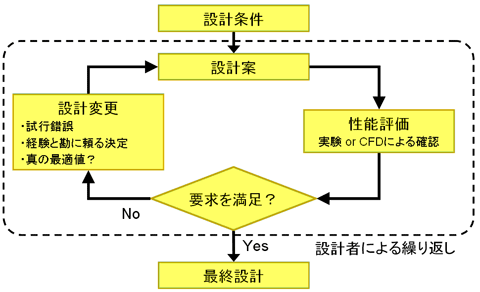 図6.1 従来の設計プロセス
図6.1 従来の設計プロセス 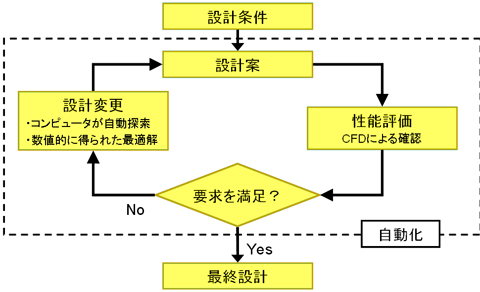 図6.2 数値解析(CFD)と最適化を用いた設計プロセス
図6.2 数値解析(CFD)と最適化を用いた設計プロセス  表6.1 ターボ機械最適化設計の目的関数選定例
表6.1 ターボ機械最適化設計の目的関数選定例 





