空気が流れる空間をメッシュで細かく刻む:実務経験者が教える! ターボ機器の設計解析の勘所(3)(1/3 ページ)
解析の頭脳「ソルバ」をうまく動かすには、適切なメッシュ作成が肝心だ。今回はメッシュの基礎から解説する
これに続く3次元流体解析(以下、CFD:Computational Fluid Dynamics)では、図3.1に示すように、大きく「メッシュ生成」「解析実行」「結果評価」の3ステップに分けることができます。今回から第5回までは、これらの3ステップについて詳しく説明したいと思います。
なお、これから3回にわたり理論的な説明はできるだけ割愛し、感覚的に分かりやすい内容で進めたいと思います。このため、厳密な理論上は若干矛盾する点や、説明不足の点もありますがご了承ください。
では今回のテーマは「メッシュ」です。流体解析では解析を実行する「ソルバ(Solver)」の方程式、離散化手法、乱流モデル、物理モデル……とさまざまな理論が存在し、設計現場ではその性能について議論されることが多いのですが、実はそのソルバの性能をいかに引き出すかはそのメッシュにかかっています。そのため、コンピュータでのシミュレーションというバーチャルな世界でも、昔ながらの職人技や、経験や勘に頼るような技術が要求され、非常に重要なものなのです。
最近では自動メッシュシステムの普及により高い精度のメッシュを作ることが手軽にできるようになりましたが、このようなシステムは長年のノウハウの結晶といえるでしょう。3次元グラフィックの上でも、メッシュを作成する作業は「表面にメッシュを張る」「空間にメッシュを切る」などとアナログな表現がよく使われます。
では一旦、ターボ機械の設計から少し外れますが、まずメッシュを作成する作業とはどういうことをするのか、解説をしていきたいと思います。
メッシュと流体解析の基本
「メッシュ」は「格子」とも呼ばれ、「メッシュ作成」とはCFDで空気や水などが流れる空間を細かく刻む作業のことをいいます。では、なぜ刻む必要があるかですが、簡単な例で説明しましょう。
図3.2のように、野原に立った木に向けて風が吹き始めたとします。左から吹き始めた風は、徐々に右に移動して、木に当たります。
では、左から吹き始めた風がどのように木まで伝わるか、この空気の流れをコンピュータでシミュレーションするのが流体解析です。
そこで、この「どのように伝わるか」をシミュレーションする方法ですが、風が流れる空間を格子状に刻むことにより、それぞれの格子点に風が伝わる状態を計算します。
まず、図3.3のように、風が流れる空間に縦横の網目を置いてみました。この網目が「メッシュ」です。
縦の列に1から9の番号を付けると、初めは風が吹き始めた状態ですので、例えば左端の列だけで風速が10m/sで、そのほかの列は0m/sの無風状態となります。
CFDではこの左端の列の状態を「境界条件」、そのほかの列の状態を「初期条件」と呼びます。そして、この境界条件の状態が初期条件の空間へどのように伝わるかを計算します。
初めに「i=2」の列に注目しましょう。列の左側は境界条件で10m/sですので、左と現在の初期条件から、この列の風速は、
(10+0)/2=5m/s
となります。
次に「i=3」の列は、左側が前の列で5m/sになっているので、
(5+0)/2=2.5m/s
です。
これを、(2.5+0)/2=1.25m/s、(1.25+0)/2=0.625m/s……と右端の列まで繰り返します。
次に2番目の列に戻ります。同じように繰り返すと、この列ではすでに前の回で5m/sになっているので、
(10+5)/2=7.5m/s
です。
そしてこれを右まで(7.5+2.5)/2=5m/s、(5+1.25)/2=3.125m/s……と繰り返します。
さらに、これを表にしてみましょう。
40回まで繰り返すと、左から吹き始めた風が右の木まで伝わっていることが分かります。
流体の流れには「質量保存則」という前提があり、これは計算領域に「入る空気」と「出て行く空気」が同じ量になるという法則です。これが成り立つまで、つまり上の例では入り口の速度と出口の速度が同じと見なされる(「収束する」といいます)まで計算を繰り返します。これをCFDでの「反復計算」といいます。密度が一定であり、入り口の面積と出口の面積が同じであると仮定すると、質量を保存するには速度が同じになる必要があります。
このように、CFDでは空気が流れる空間をメッシュで刻むことで、それぞれのメッシュの点での流れがどのようになるかを反復して計算することにより、流れがどのような状態になるかをコンピュータで計算します。
なお、ターボ機械のCFDでは、圧縮機であれば入口より出口の密度が高く、タービンでは膨張するので、その逆に出口の密度が低く、さらに入口・出口の面積は異なり、圧力や温度も異なります。よって入口と出口の質量流量(SI単位系でkg/s)で収束を判定します。
ここでは、メッシュの列の方向だけに着目しましたが、木の高さ方向については後で説明します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
 図3.1 3次元流体解析のフロー
図3.1 3次元流体解析のフロー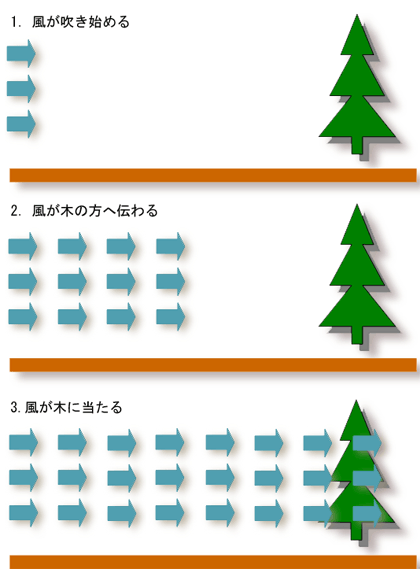 図3.2 木に吹く風
図3.2 木に吹く風 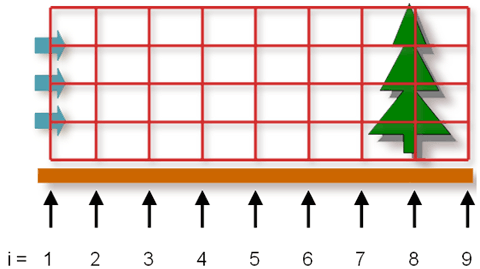 図3.3 風が吹く空間のメッシュ
図3.3 風が吹く空間のメッシュ 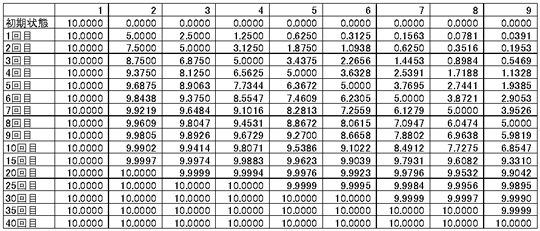 表1 風が木にどのように伝わるか?
表1 風が木にどのように伝わるか? 





