機構制御系のモデリング(その3) 〜回転2関節機構の運動学・動力学を考える〜:1Dモデリングの勘所(38)(1/5 ページ)
「1Dモデリング」に関する連載。連載第38回では「機構制御系のモデリング(その3)」と題し、回転2関節機構の運動学、動力学を考えるについて考える。
前回は“回転1関節機構系”を取り上げ、モーター、弾性アーム、質量からなる機構系で、先端(質量位置)を決められた時間で、決められた位置に移動させるという設計問題を制御も考慮して扱った。今回は運動学と動力学、順問題と逆問題の定義について述べ、その具体例として“回転2関節機構の運動学(順問題、逆問題)、動力学(順問題、逆問題)”について考える。
運動学と動力学
機構問題を扱うには大きく2つの方法がある。一つは機構の動きのみを考えるもので、「運動学(Kinematics)」と呼ばれる。もう一つは、機構が運動する際の慣性力を考慮したもので、「動力学(Kinetics)」と呼ばれる。動力学で慣性力を無視したものが運動学ともいえる。
また、各関節の動きを与えて、先端の位置を求めることを「順問題」という。一方、機構先端の位置を所定の動きにするための、各関節の動き(動力学の場合には駆動トルクも)を求めることを「逆問題」という。以上を整理すると図1となる。
運動学(順問題)
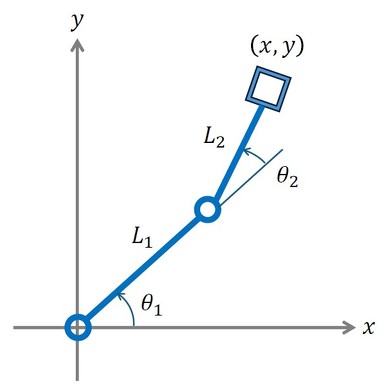
図2に示す回転2関節機構について考える。
リンク1の長さをL1、リンク2の長さをL2とし、第1関節の角変位をθ1、第2関節の各辺をθ2とすると、先端(x,y)の位置は、
となる。これが、回転2関節機構の順運動学の解となる。
一方、機械系の1Dモデリングで用いられる業界標準の表現言語「Modelica」を用いると、順運動学の式を用いてリスト1のように、数値的に解くことができる。ここでは、各関節の角変位を一定角速度で動かした場合の先端(x,y)の動きを求める。
model staticJun
import Modelica.Constants.pi;
import Modelica.Constants.g_n;
Real theta1;
Real theta2;
Real x;
Real y;
parameter Real L = 2;
parameter Real omg1 = 2*pi;
parameter Real omg2 = 2*pi;
equation
x = L*cos(theta1) + L*cos(theta1 + theta2);
y = L*sin(theta1) + L*sin(theta1 + theta2);
theta1 = omg1*time;
theta2 = omg2*time;
end staticJun;
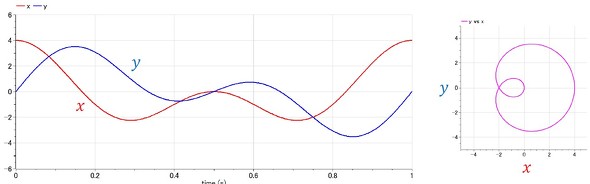
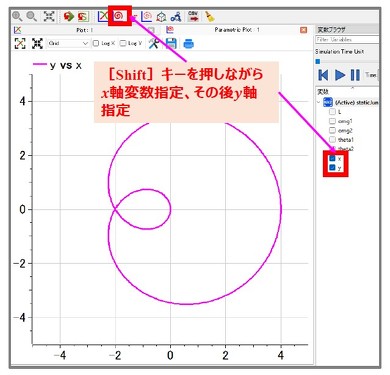
リスト1の解析例を図3に示す。図3左図は機構先端の動きの時間変化を、図3右図は横軸にx、縦軸にyを取った、いわゆる「リサージュ波形」を示す。そして、図4にオープンソースのモデリング環境「OpenModelica」でリサージュ波形を描く方法を示す。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

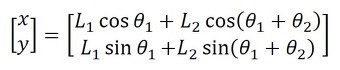 式1
式1