機構制御系のモデリング(その2) 〜回転1関節機構系を設計する〜:1Dモデリングの勘所(37)(1/4 ページ)
「1Dモデリング」に関する連載。連載第37回では「機構制御系のモデリング(その2)」と題し、回転1関節機構系の設計問題について考える。
前回は“機構と制御の基本”について説明した。これを受け、今回は具体例として“回転1関節機構系”を取り上げる。モーター、アーム、質量からなる簡単な機構系で、先端(質量位置)を決められた時間で、決められた位置に移動させるという設計問題である。運動方程式の導出、動かし方の影響、アームの剛性の影響、そして、制御の適用について説明する。
剛体軸の場合の運動方程式
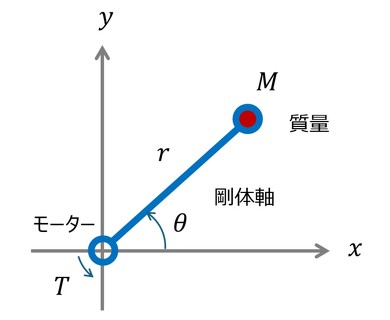
図1に剛体軸を有する回転1関節機構系を示す。根元にアームを回転駆動させるためのモーターがあり、アーム先端には集中質量があるものとする。
この系の運動方程式を導出する。モーターに関しては、
が成り立つ。このとき、Eは電圧、Vemfは起電力、Rは電気抵抗、iは電流、Lはインダクタンス、Tはトルク、Ktはトルク定数、Keは起電力係数、θは角変位、tは時間である。
一方、アームにはモーターからのトルクTが入力されるので、
が成り立つ。このとき、Jは質量Mとアーム長rから決まる慣性モーメント、Tlossは先端質量部分に作用する負荷トルクである。
通常の問題では、モーターに電圧を加えて、アームの挙動を求めるが、本問題では、アームの動かし方を決めて、その際に必要となるモーターの電圧を求めることになる。
角変位制御駆動と角速度制御駆動
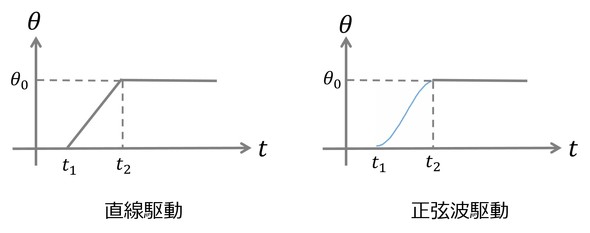
角変位θの動かし方について考える。アーム先端は時間Δtの間に、θ0角変位することが仕様として与えられているものとする。最初に、図2に示す角変位制御駆動について検討する。このとき、時刻t1で起動し、t2で停止するものとする。すなわち、Δt=t2−t1となる。駆動方法としては、直線的に角変位する直線駆動と、正弦波上に角変位する正弦波駆動を採用する。
直線駆動の場合の運動方程式を「Modelica」でテキスト表現すると以下となる(リスト1)。なお、このとき、アーム長0.05m、質量0.01kgとし、モーターに関して、R=1Ω、Ke=1.2×10-3Vs、Kt=1.2×10-3Nm/A、L=10-5H、負荷トルクTloss=10-5Nm、t1=0.1s、t2=0.2s、θ0=(π/4)radとした。
model rigidlinear import Modelica.Constants.pi; Real E; Real i; Real T; Real J; Real V; Real theta; Real thetav; Real thetaa; parameter Real R=1; parameter Real Ke=1.2e-3; parameter Real Kt=1.2e-3; parameter Real L=1e-5; parameter Real M=0.01; parameter Real r=0.05; parameter Real theta0=pi/4; parameter Real t1=0.1; parameter Real t2=0.2; parameter Real Tloss=1e-5; equation thetav=der(theta); thetaa=der(thetav); E=V+R*i+L*der(i); i=T/Kt; V=Ke*der(theta); T=J*thetaa+Tloss; J=M*r^2; theta = if (time<t1) then 0 elseif (time>=t1 and time<t2) then (theta0/(t2-t1))*(time-t1) elseif (time>=t2) then theta0 else 0; end rigidlinear;
正弦波駆動の場合は以下となる(リスト2 ※式部分のみを示す)。
model rigidcos ―――省略――― equation thetav=der(theta); thetaa=der(thetav); E=V+R*i+L*der(i); i=T/Kt; V=Ke*der(theta); T=J*thetaa+Tloss; J=M*r^2; theta = if (time<t1) then 0 elseif (time>=t1 and time<t2) then 0.5*theta0*(1-cos((pi/(t2-t1))*time-(pi/(t2-t1))*t1)) elseif (time>=t2) then theta0 else 0; end rigidcos;
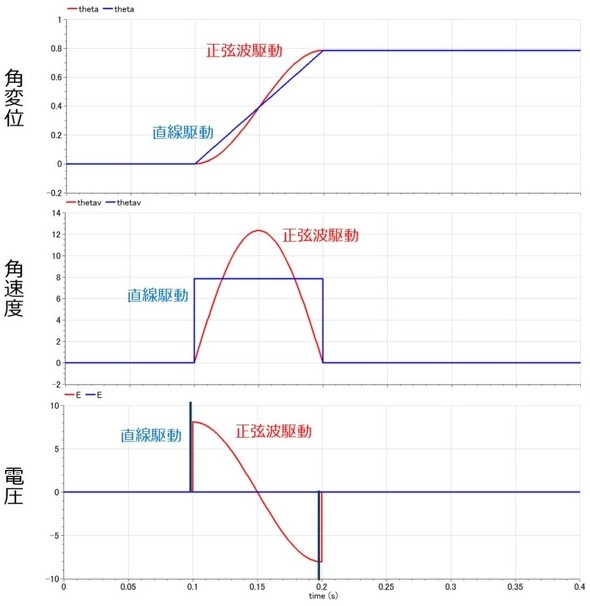
上記を解析した結果を、直線駆動と正弦波駆動で示す(図3)。角変位、角速度に関しては、波形は異なるものの、大きさは同程度である。一方、電圧は直線駆動の場合、t1=0.1で+∞、t2=0.2で−∞となり、モーターに大きな負荷がかかることが分かる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
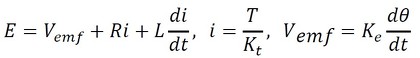 式1
式1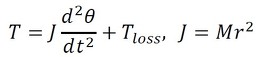 式2
式2