機構制御系のモデリング(その2) 〜回転1関節機構系を設計する〜:1Dモデリングの勘所(37)(3/4 ページ)
» 2024年11月11日 09時00分 公開
[大富浩一/日本機械学会 設計研究会,MONOist]
弾性軸の場合の運動方程式
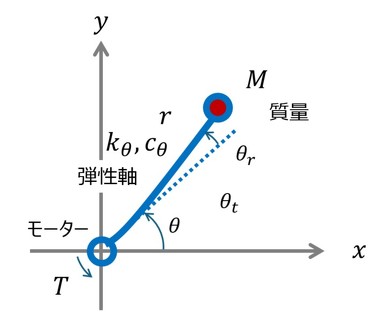
次に、アームが弾性体の場合について考える。図6に示すように、アームの回転ばね定数をkθ、回転減衰定数をcθとすると、モーターに関しての方程式は以下となる(式4以降)。
モーターに関して、
となり、モーターのトルクとアームの弾性力、減衰力のつり合いから、
となり、質量とアームから構成される振動系に関して、
となる。このとき、アームの半径をrb、アーム材料の縦弾性係数をE、損失係数をηとすると、式7が成り立つ。
以上を、Modelicaでテキスト表現すると以下となる(リスト5)。なお、E=2.1×1011Pa、rb=0.001m、η=0.003とした。
model flexNoControl import Modelica.Constants.pi; Real E; Real i; Real T; Real J; Real V; Real theta; Real thetav; Real thetaa; Real thetav0; Real Id; Real kc; Real cc; Real thetar; Real thetarv; Real thetara; Real thetat; parameter Real R = 1; parameter Real Ke = 1.2e-3; parameter Real Kt = 1.2e-3; parameter Real L = 1e-5; parameter Real M = 0.01; parameter Real r = 0.05; parameter Real Tloss = 1e-5; parameter Real theta0 = pi/4; parameter Real t1 = 0.1; parameter Real t2 = 0.13; parameter Real t3 = 0.17; parameter Real t4 = 0.2; parameter Real rr = 1e-3; parameter Real Ey = 2.1e11; parameter Real ita = 0.003; equation Id = pi*rr^4/4; kc = 2*Ey*Id/r; cc = ita*sqrt(J*kc); thetav = der(theta); thetaa = der(thetav); thetarv = der(thetar); thetara = der(thetarv); thetat = theta + thetar; E = V + R*i + L*der(i); i = T/Kt; V = Ke*der(theta); -T=cc*thetarv+kc*thetar; J*thetara + cc*thetarv + kc*thetar + Tloss = -J*thetaa; J = M*r^2; thetav0 = 1.43*theta0/(t4 - t1); thetav = if (time < t1) then 0 elseif (time >= t1 and time < t2) then 0.5*thetav0*(1 - cos((pi/(t2 - t1))*time - (pi/(t2 - t1))*t1)) elseif (time >= t2 and time < t3) then thetav0 elseif (time >= t3 and time < t4) then 0.5*thetav0*(1 + cos((pi/(t4 - t3))*time - (pi/(t4 - t3))*t3)) elseif (time >= t4) then 0 else 0; end flexNoControl;
リスト5 Modelicaでテキスト表現
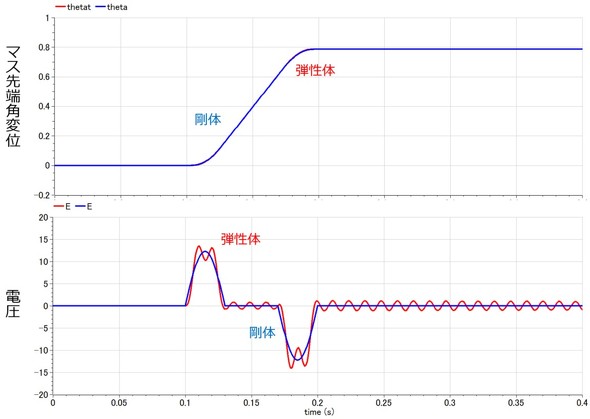
上記を解析した結果を、弾性軸と剛体軸の応答の比較として示す(図7)。駆動方法はいずれも、角速度制御駆動の正弦波駆動である。マクロにはマス先端の角変位に違いは見られないが、弾性体の場合にはアームが振動することにより、角加速度が発生し、これが電圧に影響として表れている。
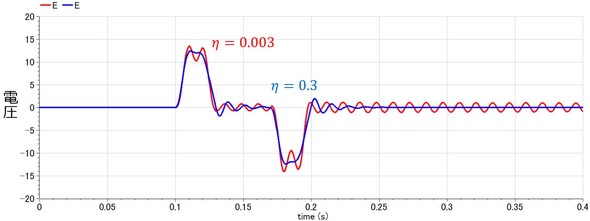
図7の弾性体では、減衰は材料自体の損失のみを考慮していたが、アーム自体に高減衰処理を行えば、見掛け上の損失係数を大きくできる。そこで、損失係数を100倍にした結果を、高減衰処理していないものと比較して示す(図8)。このように、高減衰処理を行えば電圧(角加速度)も振動的にならないことが分かる。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
Special SitePR
あなたにおすすめの記事PR
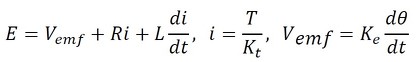 式4
式4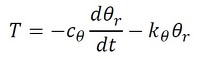 式5
式5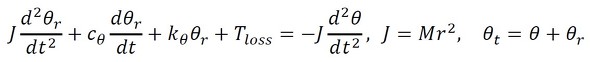 式6
式6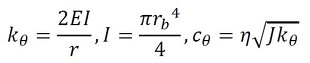 式7
式7