有限要素法入門 〜連立方程式の解法、変位の計算〜:CAEを正しく使い疲労強度計算と有機的につなげる(3)(1/7 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第3回では、前回作成した全体剛性マトリクスから弾性変形後の変位を求める。そして、変位−ひずみマトリクス[B]を導出する。
前回は、今さら誰もやらないであろう「有限要素法」の解説を始めてしまい、全体剛性マトリクスを作りました。これから弾性変形後の変位を求めましょう。そして、変位−ひずみマトリクス[B]を導出します。この辺りが1次要素と2次要素での解析精度の違いが出てくるポイントになります。
連立方程式の解法、変位の計算
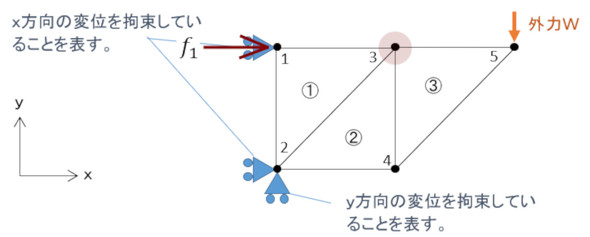
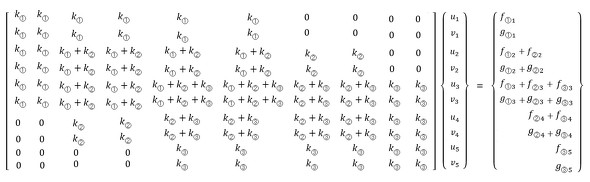
以下、連載第2回の図4を再掲し、図1とします。連載第2回の式28を再掲し、式1とします。
節点3に注目します。節点3には要素①の荷重、要素②の荷重、要素③の荷重が作用しています。式1の荷重ベクトルの上から5行目です。これらはつり合い状態にあるので荷重の和はゼロになります。次式となります。
節点1のx方向変位は拘束されているので、外界の拘束点から反力を受けています。これがf①1です。反力は未知数なので、f①1をf1と表記しましょう。節点5には−Y方向にWの外力が作用しています。次式のように表記しましょう。
f1とWを図1に記入しました。節点1のx方向変位、節点2のx方向変位、節点2のy方向変位は拘束されているので次式が成立します。
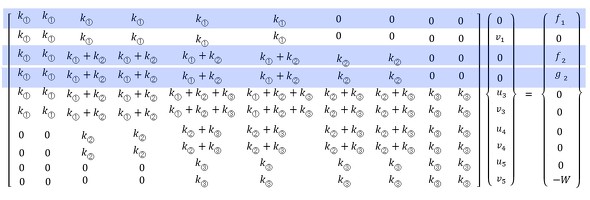
前述した関係を式1に代入しましょう。次式となります。変位が拘束されている行に色を付けておきました。
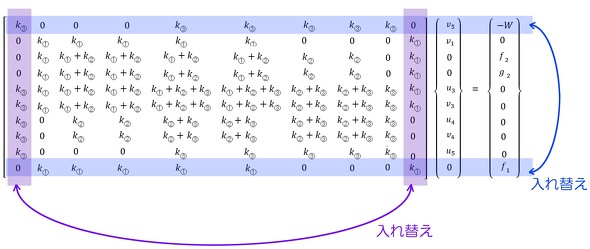
変位が拘束されている行を全て下に移動させましょう。最初に1行目と10行目を入れ替えます。次式となります。このとき、1列目と10列目を入れ替えるのを忘れないでください。
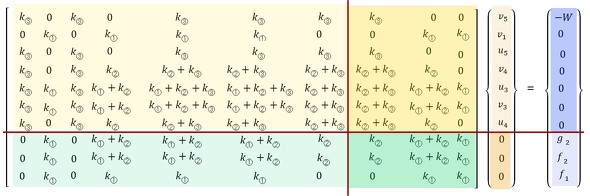
同様に3行目と9行目、4行目と8行目を入れ替えます。次式となります。
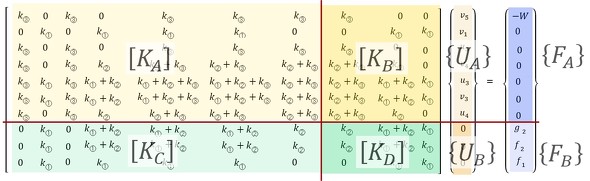
全体剛性マトリクスを4つに分解して名前を付けます。変位ベクトルと荷重ベクトルも2つに分解して名前を付けます。次式です。
名前を付けた行列とベクトルを記号で書くと次式となりますね。
上式の1行目と2行目を別々に書きましょう。
式10の行列[KA]の逆行列を求めて[KA]-1と書きます。逆行列の求め方はいろいろあるので読者の皆さんが習った方法で行ってください。式10の左辺第2項を右辺に移して、両辺に左側から[KA]-1を掛けます。次式です。
[KA]-1[KA]は単位行列になるので上式は以下となって、各節点の変位が求まりました。
上式の{UA}を式11に代入すると{FB}、つまり拘束点の反力が求まります。次式です。
ここでの説明は{UB}の各行はゼロだったのですが、拘束点ではなく強制変位を掛けたいときはその数値が{UB}となります。
以上の操作で各節点の変位が求まりました。このように節点変位を先に求める方法を「変位法」と呼びます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

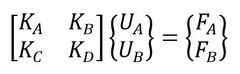 式9
式9





