有限要素法入門 〜連立方程式の解法、変位の計算〜:CAEを正しく使い疲労強度計算と有機的につなげる(3)(2/7 ページ)
マトリクス材料力学
今まで述べてきた方法は、狭い意味での有限要素法ではありません。単なる連立方程式の解法です。
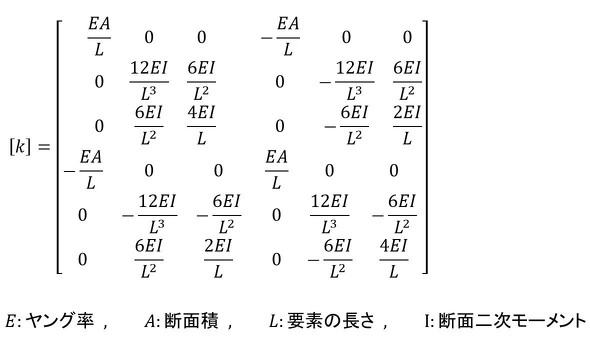
例えば、図2はラーメン構造解析の例ですが、前述した方法と全く同じ方法で計算しています。要素剛性マトリクスは式15で表されていて、左上の要素は単なる「フックの法則」、それ以外の要素は「はりの曲げ理論」で求まっています。こういうものを「マトリクス材料力学」とでも呼べばよいのでしょうか。
ひずみの計算
図3に要素の変形を示します。「要素の変形」ではなく「節点の変位」と表現してもよいかと思います。
図3左側の場合は要素が移動しただけです。平行移動しただけなので要素にひずみは発生していません。3つの変位ベクトルは同じ値を持ちます。次式です。
図3右側の場合は要素が伸ばされています。要素が弾性変形しているとすると、ひずみが発生しています。各節点の変位は異なる値を持つので次式となります。
以上のことから、節点変位を使って要素に発生しているひずみが求まりそうですね。では、丸棒の場合を考えてみましょう。図4に丸棒が伸ばされた状態を示します。
一端(O点)が固定されていて、多端(A)が引き延ばされてA’に移動したとします。移動量をδと書きます。δは伸びた量ですね。この棒のひずみは次式で表されます。
棒の端からxの位置の変位を求めます。変位は位置xの関数としてu(x)と表記します。以下の関係式が成り立ちます。
u(x)は位置xに比例するので、任意の位置の変位は次式で表されます。
式19と式20を、式21に代入したらその通りになりますね。では、式21をxで微分しましょう。以下となります。
変位を座標で微分すると、ひずみとなりました。2次元問題では任意の位置のx方向変位をu(x,y)、y方向変位をv(x,y)とすると、ひずみは次式となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

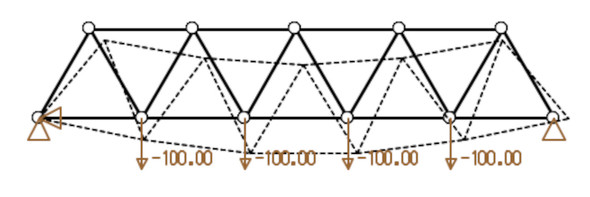
 式15
式15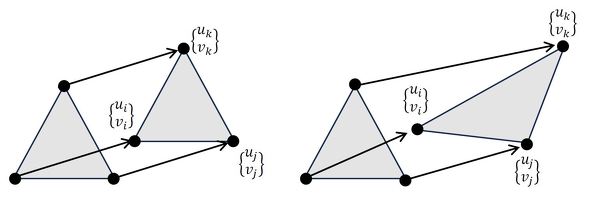
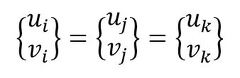 式16
式16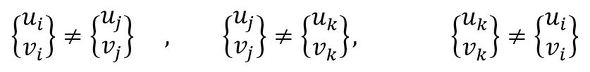 式17
式17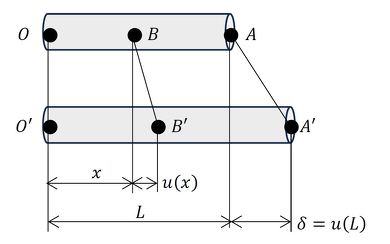
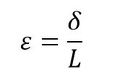 式18
式18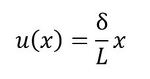 式21
式21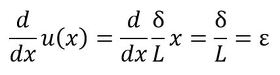 式22
式22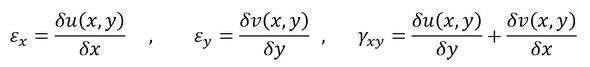 式23
式23





