有限要素法入門 〜連立方程式の解法、変位の計算〜:CAEを正しく使い疲労強度計算と有機的につなげる(3)(3/7 ページ)
» 2024年04月15日 09時00分 公開
[高橋良一/RTデザインラボ 代表,MONOist]
要素内部の変位を式で表そう
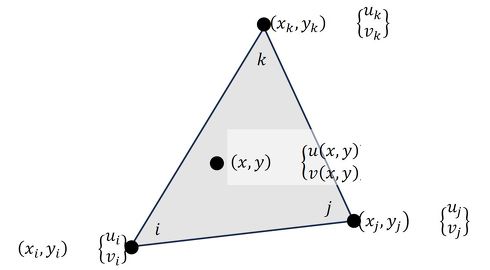
図5に示した要素内部の任意の点(x,y)の変位を求める式を作りましょう。この式が有限要素法の解析精度を決定づけます。
手掛かりとなる情報は以下の6つです。
- i節点において、つまり座標(xi,yi)において、x方向変位はuiである
- i節点において、つまり座標(xi,yi)において、y方向変位はviである
- j節点において、つまり座標(xj,yj)において、x方向変位はujである
- j節点において、つまり座標(xj,yj)において、y方向変位はvjである
- k節点において、つまり座標(xk,yk)において、x方向変位はukである
- k節点において、つまり座標(xk,yk)において、y方向変位はvkである
要素内部の任意の点(x,y)の変位を求める式を次式としましょう。
先に答えを言っておくと、式24と式25はx,yの1次式です。よって、このような要素を「1次要素」といいます。未知数はα0,α1,α2,β0,β1,β2と6個、手掛かりとなる情報も6個です。連立方程式を解けば式24、式25が作れそうです。連立方程式は以下となります。
3元連立方程式が2セットになりました。式26-1、式26-2、式26-3をマトリクス表示すると次式となります。
行列式を使った連立方程式を求める方法を使います。未知数は次式となります。
β0,β1,β2も同じ方法で求まりますね。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン社員が技能五輪国際大会の工業デザイン技術職種で日本代表に
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
Special SitePR
あなたにおすすめの記事PR

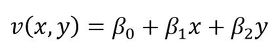 式25
式25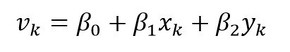 式26-6
式26-6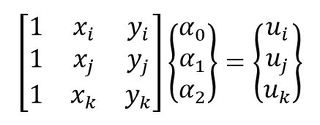 式27
式27 式28
式28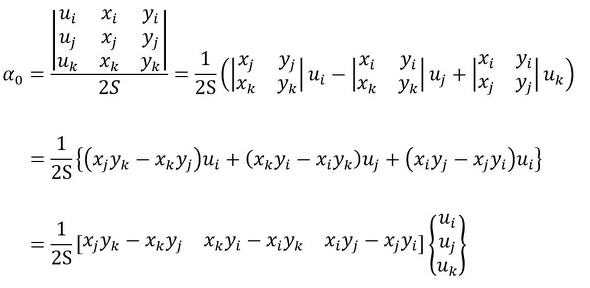 式29
式29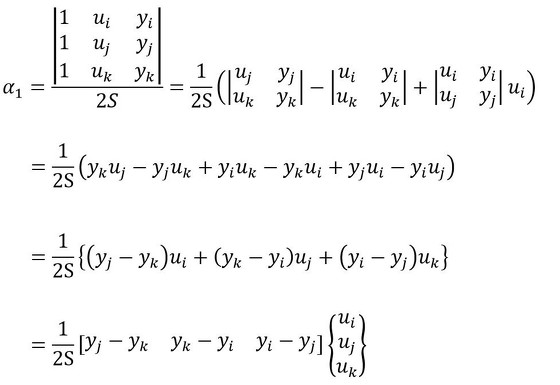 式30
式30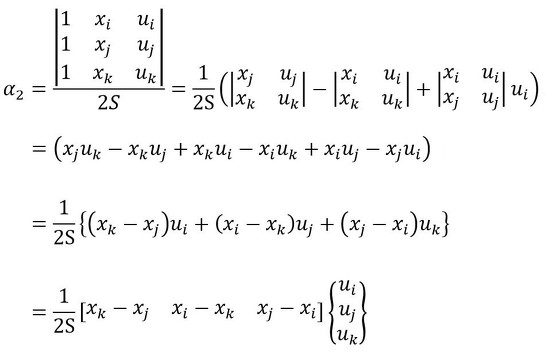 式31
式31





