有限要素法入門 〜連立方程式の解法、変位の計算〜:CAEを正しく使い疲労強度計算と有機的につなげる(3)(6/7 ページ)
レイリー・リッツ法とガラーキン法
有限要素法は「実は『レイリー・リッツ法(Rayleigh-Ritz method)』なのだよ」や「実は『ガラーキン法(Galerkin method)』なのだよ」といったことが書かれている文献やWebサイトがあります。筆者が講義を受けた当時は「レーレー法」と先生は呼んでいました。
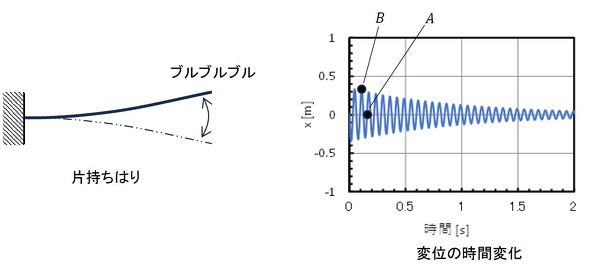
では、レーレー法について、片持ちはりを例に説明していきましょう。ここでは片持ちはりの固有振動数を求める問題です。図7に、片持ちはりを指で変形させて、その後指を放した後の先端変位の時間変化を示します。片持ちはりは「ブルブルブル」っと振動します。このときの振動数をレ−レー法で求めてみましょう。
レーレー法の弾性変形問題での戦略は以下となります。
- 変形形状を簡単な関数で仮定する
- エネルギーを計算し、エネルギー保存やポテンシャルエネルギー最小などの規則を用いて所望の解を得る
参考文献[5]では、形状をxの3次式で仮定していますが、ここでは変形形状を次式(コサインカーブ)で仮定してみましょう。式50を図示したものが図8にとなります。コサインカーブも片持ちはりの変形のようですね。
次のステップは、エネルギーの計算です。図7右図に注目します。A点の変形量はゼロですが、速度は最大です。B点は振動の折り返し点なので速度はゼロで、変形量は最大です。エネルギー式として次式が成立します。エネルギー保存則となります。
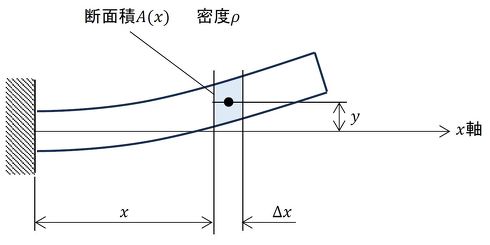
では、運動エネルギーを求めましょう。図9に座標と変形形状の関係を示します。
位置xで長さ∆xのはりの微小な一部に注目します。断面積をA(x)、密度をρとすると、はりの微小な一部の質量はρA(x)∆xで、速度は変位yを時間で微分したものなので、次式で表されます。
はりの微小な一部の運動エネルギーは次式となります。
これをはりの全長で積分したものがはり全体の運動エネルギーで、次式となります。∆xをdxに書き換えました。また、断面積はxの関数でしたが一定値Aとします。
変形量がゼロのとき速度は最大です。cos ωt=1のときに運動エネルギーは最大となり次式となります。次式です。
では、速度ゼロのときの弾性変形のエネルギーを求めましょう。以前の連載「フリーFEMソフトとExcelマクロで形状最適化」で弾性体に蓄えられるひずみエネルギーは次式で表されると述べました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dモデリングツールの積層造形を支援する機能アップデート
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 幾何公差の基準「データム」を理解しよう
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 再使用型宇宙機の開発にクラウドネイティブなCAD/PDMプラットフォームを採用

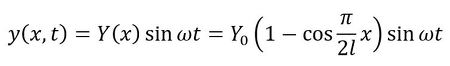 式50
式50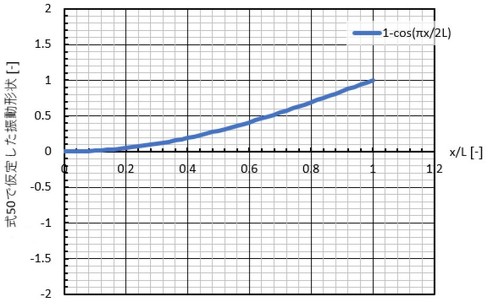
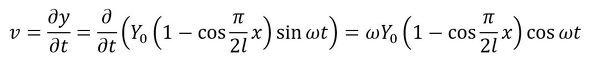 式52
式52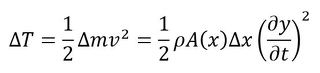 式53
式53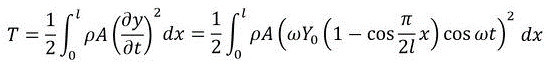 式54
式54 式56
式56





