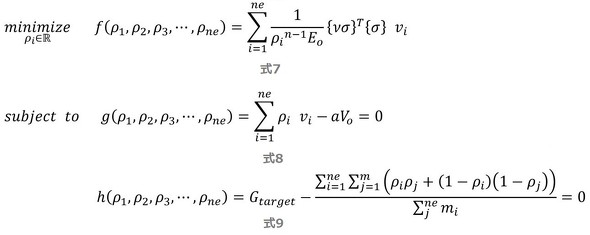トポロジー最適化のチェッカーフラグ対策:フリーFEMソフトとExcelマクロで形状最適化(9)(2/6 ページ)
» 2022年05月17日 07時00分 公開
[高橋良一/RTデザインラボ 代表,MONOist]
チェッカーフラグ対策の方法
チェッカーフラグ対策のアルゴリズムは、大まかに分けて2種類あります。1つ目はペナルティーを科すという考え方で、2つ目はラグランジュの未定乗数法の制約関数を追加する方法です。
1つ目の方法を説明します。目的関数が最小になるような設計変数を求めているため、チェッカーフラグになったら目的関数が増えるようにペナルティーを付加すればよいことになります。図2に示したように、チェッカーフラグがない状態の場合、Gは大きくなるのでマイナスの符号を付けて目的関数に追加します。参考文献[1]では、目的関数f(ρ1,ρ2,ρ3……ρne)として次式が提案されています。
この方法を行うには有限要素法ソフトを自分で作る覚悟が必要です。今回の趣旨はフリー有限要素法ソフト「LISA」を使って最適化を行うことでしたので、1つ目の方法は採用できません。
2つ目の方法を説明します。連載第3回で、ラグランジュの未定乗数法では制約関数を幾つでも追加できることを述べました。式4で計算される重力関数に、目標値Gtargetを設定しましょう。制約関数hは次式となります。式1のpは自分で決めてよいので、p=1とします。
ラグランジュ関数は次式となります。
トポロジー最適化問題は以下のように表現できます。
viは、各要素の見掛けの体積です。各要素は軽石のようにスカスカ状態で内部空洞を含めた体積です。Voは、最適対象全体の見掛けの体積です。aは目標とする体積比率で、実際の体積と見掛けの体積の比となります。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR

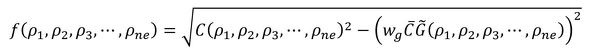 式3
式3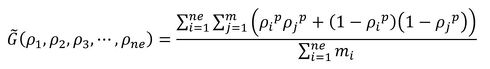 式4
式4 式4の補足
式4の補足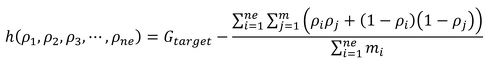 式5
式5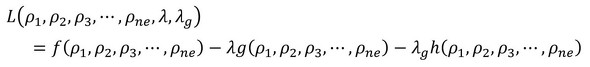 式6
式6