剛性を最大化するはりの形状を求める:フリーFEMソフトとExcelマクロで形状最適化(3)(1/3 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第3回では、片持ちはりの平均コンプライアンス最小化問題を「ラグランジュの未定乗数法」を使って解いていく。
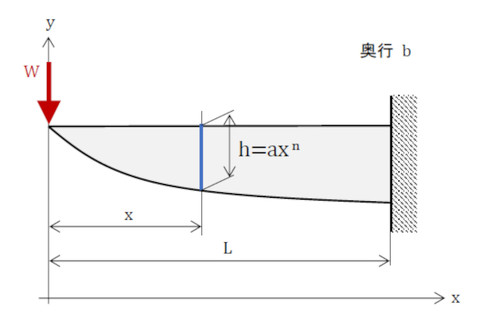
先端に荷重が作用する“片持ちはり”で、変形量を最小化(=剛性を最大化)する、つまり平均コンプライアンスを最小化するはりの形状を求めましょう。はりの形状は図1、式1のような形状に限定します。
そして、hについては、aを大きくすれば単純に変形量が小さくなるのは分かっているので、「はりの体積がVoである」という制約を入れましょう。これらの条件を満たすnとaを求める問題です。
ラグランジュの未定乗数法
「ラグランジュの未定乗数法」(参考文献[1])を説明します。荷重Wが作用したときのコンプライアンスf(n,a)は式2でした。
体積がVoであるという制約条件は式3でした。
式3を満足させながら、平均コンプライアンスf(n,a)が極小となるnとaを求める問題を解くには、次に示すラグランジュ関数Lを導入します。ここでλは、「ラグランジュ乗数」と呼ばれる定数です(式4)。
そして、次式(式5〜7)で示す連立方程式を解けば、f(n,a)が極小となるnとaが求まります。
「f(n,a)が極小となる」と書きましたが、これはf(n,a)が下に凸の関数である場合です。f(n,a)が上に凸の関数のときは極大となります。
ラグランジュの未定乗数法をもう少し一般的に説明しましょう。パラメトリック最適化の対象となる設計変数がm個ある場合、設計変数は以下のように表現できます(式8)。
そして、極小値ないしは極大値としたい目的関数は式9で表されます。
制約条件がn個あるとします。その際、以下に示すようにn個の等式があることになります(式10-1〜10-n)。
ラグランジュ関数Lは式11となります。
総和の記号Σを使うと、ラグランジュ関数Lは次式となります(式12)。
fが極小ないし極大となるρiを求めるには、次に示した連立方程式を解くことになります(式13、式14)。
式13はm個あり、式14はn個あります。一方、未知数は、ρiがm個、λjがn個あって、未知数と式の数が一致するので、fを極小化ないしは極大化する変数ρ1、ρ2、ρ3……ρmが求まることになります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞

 式1
式1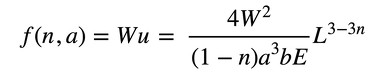 式2
式2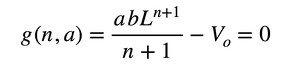 式3
式3 式5
式5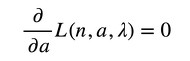 式6
式6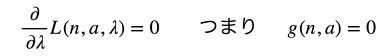 式7
式7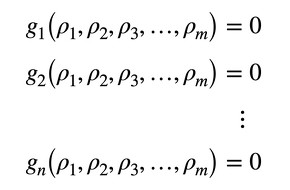 上から式10-1/式10-2/式10-n
上から式10-1/式10-2/式10-n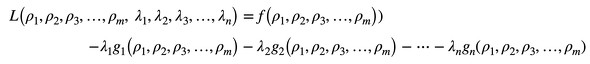 式11
式11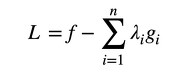 式12
式12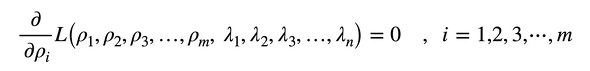 式13
式13





