剛性を最大化するはりの形状を求める:フリーFEMソフトとExcelマクロで形状最適化(3)(2/3 ページ)
» 2022年02月07日 10時00分 公開
[高橋良一/RTデザインラボ 代表,MONOist]
平均コンプライアンスを最小化、剛性を最大化するはりの形状
それでは、ラグランジュの未定乗数法を使って、平均コンプライアンスを最小化、つまり剛性を最大化するnとaを求めましょう。
ラグランジュ関数L(式4)は次式となります(式15)。
式5を計算しましょう(式16)。
第1項のL3-3nの微分は以下のようにします(式17)。
両辺を微分します(式18)。
2つの関数の商の微分公式は次式でした(式19)。
よって、式16は以下のようになります(式20)。
「こんな微分は学生のときにやって以来で、社会人になって初めてだ!」という方もおられると思いますが、少しお付き合いください。
式6を計算しましょう(式21)。
式20を式21で割り算します(式22)。
n=1/2となりました。式1は次のようになります(式23)。
あれ、どこかで見た式ですね。“平等強さのはり”と同じ結果となりました。平等強さのはりは、剛性最大のはりでもありました。こんなことは材料力学の講義では習いませんでした。筆者も本連載を書きはじめて知りました。
では、aを求めましょう。
式3に式23を代入します(式24)。
λを求めましょう。式21に式23、式24を代入します(式25)。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
Special SitePR
あなたにおすすめの記事PR

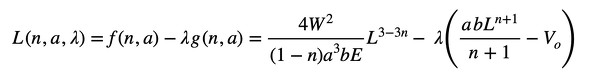 式15
式15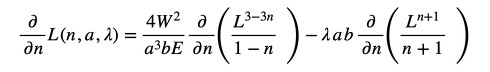 式16
式16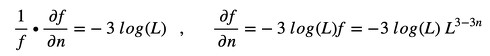 式18
式18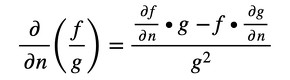 式19
式19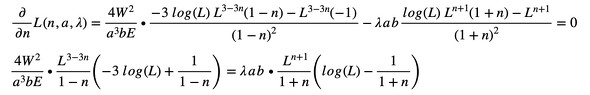 式20
式20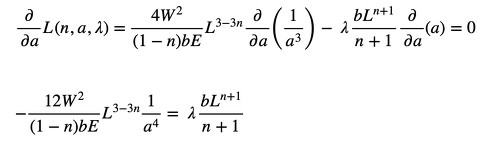 式21
式21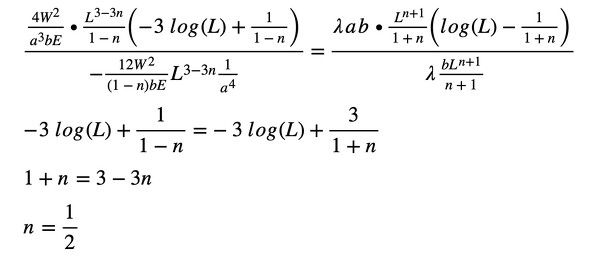 式22
式22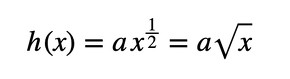 式23
式23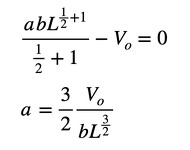 式24
式24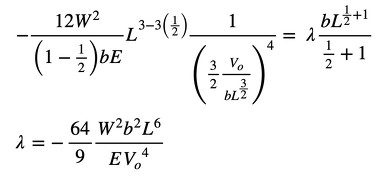 式25
式25





