トポロジー最適化のチェッカーフラグ対策:フリーFEMソフトとExcelマクロで形状最適化(9)(1/6 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第9回では、チェッカーフラグ状の濃淡とグレーの濃淡をなくす方法を紹介する。
これまで述べてきた方法では、ソフトウェアが出力する最適化形状にチェッカーフラグ状の密度ρiの濃淡が現れました。トポロジー最適化は、「チェッカーフラグ状の濃淡、白黒はっきりしないグレー、小骨は悪」として発展しますが、その結果、境界のはっきりした最適化形状が求まるようになりました。今回は、チェッカーフラグ状の濃淡とグレーの濃淡をなくす、1つの方法を紹介します。
チェッカーフラグの度合いと、白黒はっきりしない度合いの数値化
「ラグランジュの未定乗数法」を使って目的関数が最小になる設計変数を求めているため、チェッカーフラグの度合いと、白黒はっきりしない度合いを数値化する必要があります。参考文献[1]では、その度合いの指標として次式が提案されています。「gravity control関数(重力関数)」と呼びます。
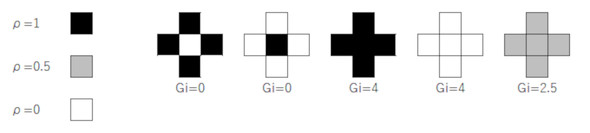
上式において、iは要素番号、jは要素番号iの要素の周辺の要素に番号を付けたものです。例えば、周辺の要素を上下左右の要素と決めた場合、図1に示すように、jは1、2、3、4となり、m=4となります。
式1、式2のpは自分で決められる定数です。参考文献[1]ではp=2としています。Giの幾つかの例を図2に示します。チェッカーフラグ状態ではGi=0と小さい値となり、ρiの全てが0か1の状態、つまり白黒はっきりした状態ではGi=4と大きくなります。また、グレー状態はGi=2.5と中間的な値となります。ρiの初期値は、例えば全てのρiに対して0.375[-]とするため、全体がグレーとなります。これは図2右の状態で、Giは理想の4よりも小さな値となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

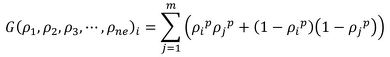 式1
式1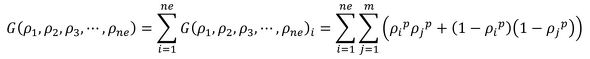 式2
式2