位置公差の総仕上げと振れ公差について　～曖昧さを取り除く幾何公差～：産機設計者が解説「公差計算・公差解析」（15）（4/4 ページ）

» 2020年05月07日 10時00分 公開
前のページへ 1|2|3|4 　　　　　　

3－2．全振れ（Total runout）

　次に全周振れについて、JISで確認してみると、

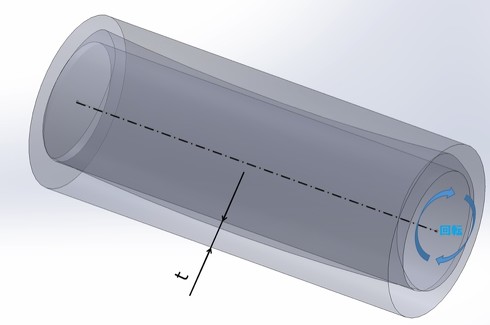
データム軸直線を軸とする円筒面を持つべき対象物またはデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した方向に変位する大きさをいう

と定義されています。

  • 公差域の定義
    　公差域は、tだけ離れ、その軸線はデータムに一致した2つの同軸円筒によって規制される。
全周振れの公差域 図15　全周振れの公差域 ［クリックで拡大］
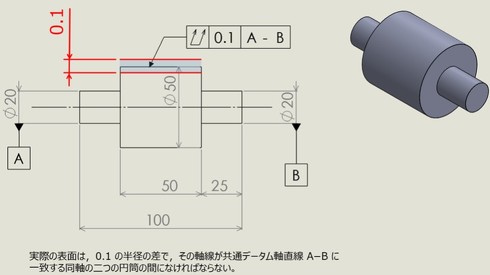
全周振れの使用例（ラジアル方向） 図16　全周振れの使用例（ラジアル方向） ［クリックで拡大］

　全周振れでは、その幾何公差が指示された「円筒表面全体がデータム軸と同軸となる幅（図16では0.1［mm］）の2円筒間にあること」を示します。また、円周振れと同じく、全周振れについてもアキシャル方向を使用し、ラジアル方向と同様に、全周振れが指示された「円筒端面全体についてデータム軸と直角な幅の2面間にあること」を示します。


　長期間にわたり、幾何公差についてJISを参考にしながら解説を行ってきました。幾何公差は、サイズ公差だけでは曖昧な形体から、曖昧さを取り除きます。今後主流になっていく「公差設計」と「幾何公差＝GD＆T（Geometric Dimensioning＆Tolerancing：幾何公差設計法）」を実践する上では、幾何公差を学んでいくことが必須になります。皆さん、ぜひ一緒に学んでいきましょう！ （連載完）

Profile

土橋美博（どばし・よしひろ）

1964年生まれ。25年間、半導体組み立て関連装置メーカーで設計・営業・3次元CAD推進を行う。現在、液晶パネル製造装置を主体に手掛ける株式会社飯沼ゲージ製作所で3次元CADを中心としたデジタルプロセスエンジニアリングの構築を推進する。ソリッドワークス・ジャパンユーザーグループ（SWJUG）の代表リーダー・事務局も務める。


前のページへ 1|2|3|4 　　　　　　

Copyright © ITmedia, Inc. All Rights Reserved.