位置公差の総仕上げと振れ公差について 〜曖昧さを取り除く幾何公差〜：産機設計者が解説「公差計算・公差解析」（15）（2/4 ページ）

[土橋美博／飯沼ゲージ製作所，MONOist]

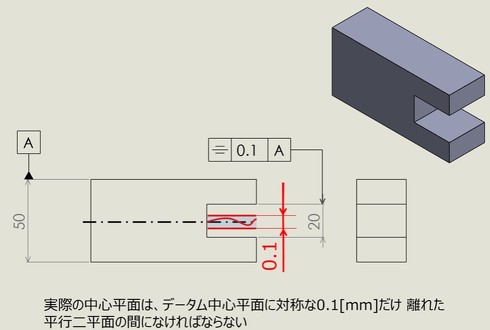
2−4．対称度（Symmetry）

　続いて「対称度」ですが、JISによると、

データム軸直線またはデータム中心平面に関して互いに対称であるべき形体の対称位置からの狂いの大きさをいう

と定義されています。

• 公差域の定義
  　公差域は、tだけ離れ、データムに関して中心平面に対称の平行2平面によって規制される。

図7　対称度の公差域 ［クリックで拡大］

図8　対称度の使用例 ［クリックで拡大］

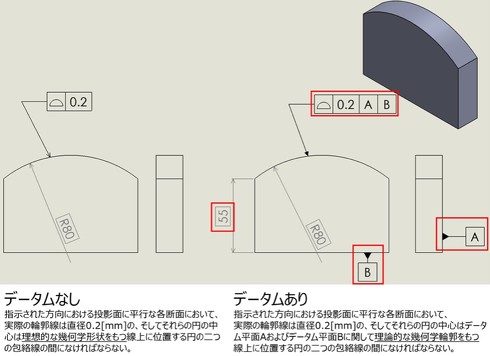
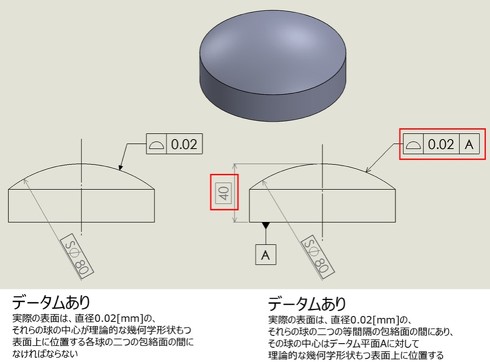
2−5．データムに関連した輪郭度

　線の輪郭度、面の輪郭度については、データムに関連しない場合の「形状公差」でその説明を行っています。データムに関連する場合の公差域の定義を以降で示します。なお、データム有無における比較については、使用例の図面を利用しています。

2−5−1．線の輪郭度（Profile of a line）

• 公差域の定義
  　公差域は、直径tの各円における2つの包絡線によって規制され、それらの円の中心はデータム平面Aおよびデータム平面Bに関して理論的に正確な幾何学形状を持つ線上に位置する。

図9　線の輪郭度の使用例 ［クリックで拡大］

2−5−2．面の輪郭度（Profile of a surface）

• 公差域の定義
  　公差域は、直径tの各球における2つの包絡面によって規制され、それらの球の中心はデータム平面Aに関して理論的に正確な幾何学形状を持つ表面上に位置する。

図10　面の輪郭度の使用例 ［クリックで拡大］

　線の輪郭度も面の輪郭度も、データムがある場合とない場合の違いが分かりにくいかもしれませんが、データムがある場合は形状公差とは異なり、「相対比較するための基準」があります。