データムを必要とする幾何公差【その3】〜姿勢公差の傾斜度〜:産機設計者が解説「公差計算・公差解析」(10)(1/4 ページ)
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第10回はデータムを必要とする幾何公差をテーマに、姿勢公差の傾斜度について取り上げる。
「データム(Datum)」を必要とする姿勢公差の5つの幾何公差のうち、今回は「傾斜度」について取り上げます。
傾斜度とは何でしょうか? 少々分かりづらいと感じる人もいるかもしれませんが、次のようにその用途を考えてみると理解しやすいのではないでしょうか。
姿勢公差に分類される幾何特性において、
- 「平行度」は0度(あるいは180度)
- 「直角度」は90度(あるいは270度)
を規定しますが、傾斜度はそれ以外の任意の角度を規定するものです。
1−3.傾斜度(Angularity)
では、傾斜度の定義を見てみましょう。「JIS B 0621:1984 幾何偏差の定義及び表示」(以下、JIS)によると、
データム直線またはデータム平面に対して理論的に正確な角度を持つ幾何学的直線または幾何学的平面からの理論的に正確な角度を持つべき直線形体または平面形体の狂いの大きさをいう
と定義されています。
これまで、データム直線またはデータム平面に対して、平行である場合や直角(90度)となる場合の許容値について解説してきましたが、傾斜度は許容値を指定する直線や平面が90度以外である場合に、データムに対して正確に傾斜しているかという許容値を表します。直角度と同様、その許容値を示す数値の単位は[mm]であり、[度]ではありません。
傾斜度の表示方法は3種類あります。それぞれ順番に見ていきましょう。
1−3−1.直線形体のデータム直線に対する傾斜度
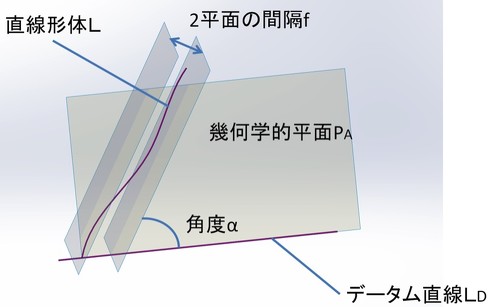
(1)同一平面にある場合の傾斜度
・公差域の定義(JIS原文、以下同様)
同一平面上にあるべき直線形体のデータム直線に対する傾斜度は、直線形体(L)のいずれか一端とデータム直線(LD)とを含む幾何学的平面(PA)に垂直で、データム直線(LD)に対して理論的に正確な角度(α)をなす幾何学的平行2平面で直線形体(L)を挟んだときの、2平面の間隔(f)で表す。
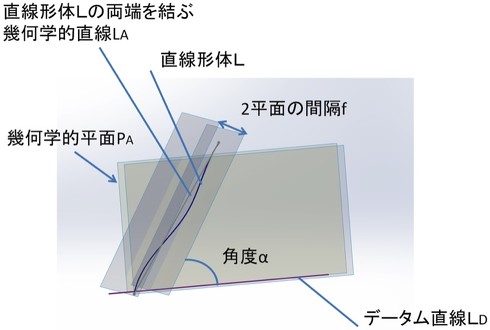
(2)同一平面上にない場合
・公差域の定義(JIS原文、以下同様)
同一平面上にない直線形体のデータム直線に対する傾斜度は、直線形体(L)の両端を結ぶ幾何学的直線(LA)に平行で、データム直線(LD)を含む幾何学的平面(PA)に垂直で、データム直線(LD)に理論的に正確な角度(α)をなす幾何学的平行2平面でその直線形体(L)を挟んだときの2平面の間隔(f)で表す。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 【レベル9】アセンブリ図面を作成せよ!
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 【調査レポート】設計・解析業務におけるAI活用の現実と課題
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 幾何公差の基準「データム」を理解しよう