データムを必要とする幾何公差【その4】〜姿勢公差の輪郭度〜:産機設計者が解説「公差計算・公差解析」(11)(1/3 ページ)
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第11回はデータムを必要とする幾何公差をテーマに、姿勢公差の輪郭度について取り上げる。
「データム(Datum)」を必要とする姿勢公差の5つの幾何公差のうち、今回は「輪郭度」について取り上げます。
1−4.輪郭度(Profile)
輪郭度の定義を「JIS B 0621:1984 幾何偏差の定義及び表示」(以下、JIS)で確認してみると、輪郭度には「線の輪郭度」と「面の輪郭度」があることが分かります。ちなみに、“データムに関連しない線の輪郭度”については、以前解説した通りです。
1−4−1.線の輪郭度(Profile of a line)
- 公差域の定義(JIS原文、以下同様)
理論的に正確な寸法によって定められた幾何学的に正しい輪郭(以下、幾何学的輪郭という)からの線の輪郭の狂いの大きさをいう。なお、データムに関連する場合と関連しない場合とがある。
補足説明:
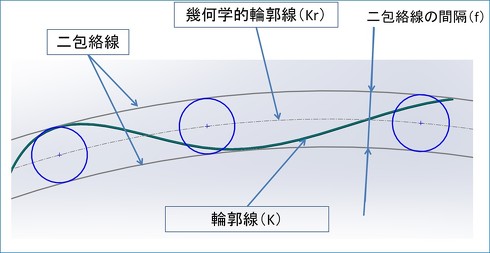
線の輪郭度は、曲面を構成する線要素(輪郭線)のバラつきを2次元の平面的な公差域で規制します。例えば、「意匠面(デザイン)などの曲面が、設計者の意図した通りにできているか」を指示する際に使用されます。指定の曲面を切断した断面の線が、公差域に含まれている必要があります。
線の輪郭度は、理論的に正確な寸法によって定められた幾何学的輪郭線(Kr)上に中心を持つ同一の直径の幾何学的円の2つの包絡線で、その線の輪郭(K)を挟んだときの、2包絡線の間隔(f)(円の直径)で表し、線の輪郭度_mmまたは線の輪郭度_μmと表示する。ただし、理論的に正確な寸法は、データム線またはデータム面に関して与える場合と、それらと関係しないで与える場合とがある。
※包絡線:ここでは、輪郭線の全てに対して接する曲線のことをいう。
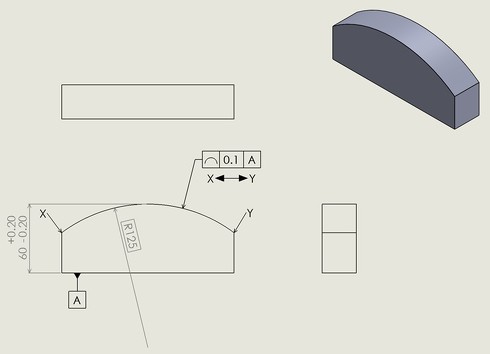
以下に、線の輪郭度の使用例を示します(図2)。
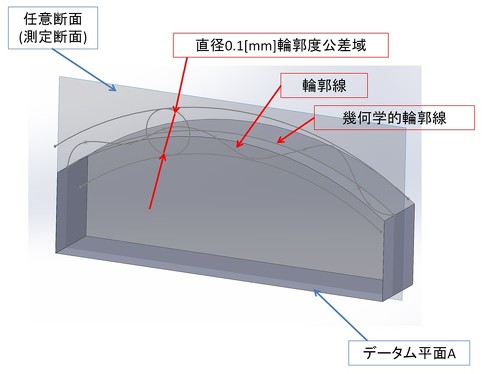
データム平面Aに垂直な任意断面(測定断面)において、実測した輪郭線は、直径0.1mmの円の2つの包絡線で規制される公差域になければならないことと、公差域はサイズ公差の範囲内(59.8〜60.2mm)で、上下方向に移動できることを示しています。その包絡線を作る円の中心は、理論的に正確なR125mmの曲率半径を持ち、かつデータム平面Aに関して理論的に正確な輪郭を成す線上にあります。つまり、実測した輪郭線には、幾何形状の規制とデータム平面Aに対する姿勢の規制が課せられています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 協働ロボット型ペレット式3Dプリンタの基本構造「バトラー方式」で特許を取得
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 3Dスキャンで伝統茶杓をデータ化、実物1点にデータ1点をひも付けて真贋証明
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化