伝熱問題や振動問題をラプラス変換を使って解く:無償ソフトで技術計算しよう【制御工学基礎編】(2)(2/2 ページ)
振動問題
プロセス系に対して、物体の運動に関する制御では、図2に示すような質量とバネとダンパの組み合わせで表される現象が多くあります。図2をモデル化してみましょう。
(3)式に演算子を施してみます。
制御工学では、初期条件は0として扱うため、(3)式の第2項は0となり、下記のようになります。
振動問題などの運動系では、(4)式の形になることがほとんどで、「二次遅れ系」と呼ばれます。
さて、(4)式右辺は下記のように書き換えることが可能で、
2つの一次遅れ系の組み合わせと考えることが可能です。ただし、複雑な式となるため、一般には分解せずに、二次遅れ系のまま扱います。
表1の2段目のデルタ関数とは、無限大の負荷が無限小の時間だけ持続するもので、現実には、ハンマなどで物体をたたいた状態が相当します。デルタ関数に演算子を施した結果が1になるということは、伝達関数はハンマなどの衝撃に対する出力ということになります。つまり、伝達関数を原関数に逆変換すれば、衝撃に対する応答が得られます。これは、インパルス応答と呼ばれます。では、(5)式の伝達関数を逆変換して、インパルス応答を求めてみます。表1の5段目を用いると、下記の式が得られます。
m=1、c=2、k=3として、tに対するyの変化をFreeMatで計算してみます。
ex503.mを動作させると、図3に示すインパルス応答が得られます。
clear;
m=1;c=2;k=3;
t=0:0.01:10;
cmk=(c^2-4*m*k)^0.5;
y=m/cmk*(exp(-(c-cmk)/2/m*t)-exp(-(c+cmk)/2/m*t));
plot(t,y);
grid('on');
xlabel('Time[s]');ylabel('Response');
答えは得られますが、もう少しスマートな方法はないものでしょうか?
実は、(6)式のexp内の係数は、m・s2+c・s+k=0の解になっています。また、全体の係数は、2つの解の差の逆数となっています。FreeMatは任意の次数の方程式を解くコマンドrootsを持っているので、これを使ってプログラムを作成してみます。
ex504.mがそのプログラムで、3行目roots([m,c,k])でm・s2+c・s+k=0の解を計算しています。rootsコマンドは、多項式の係数を高次の項から順に配列として与えると、解を配列として返します。
例えば、
--> roots([1,3,2])
とすると、s2+3s+2=0の解が、ans=−2−1として得られます。
ex504.mを動作させると、図3と同じ結果が得られます。
clear;
m=1;c=2;k=3;
x=roots([m,c,k]);
t=0:0.01:10;
y=1/(x(1)-x(2))*(exp(x(1)*t)-exp(x(2)*t));
plot(t,y);grid('on');
xlabel('Time[s]');ylabel('Response');
次回は、ブロック線図について説明します。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
- 「制御工学」豊橋技術科学大学制御工学教育連携プロジェクト著、実教出版刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
関連記事
 無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフト「FreeMat」をインストールしよう
無償の工学計算ソフトでも、かなり高度な計算ができる! 今回はインストール編。工学計算の初心者もぜひチャレンジしよう。 数式を使わないで自動制御について教えるよ
数式を使わないで自動制御について教えるよ
数式がいっぱい出てくる制御理論の習得に挫折した人は多いカモ。制御のエッセンスだけなら数式がなくても理解できる! 組み込みソフト開発の“主役”は誰に?
組み込みソフト開発の“主役”は誰に?
かつて、組み込み機器用ソフトウエアの開発は、それを専門とする技術者の手で行われていた。しかし、現在は、モデルベース設計ツールをはじめとした設計の抽象度を高めることが可能なツールを利用することで、システム設計者やドメインエキスパートであっても、組み込みソフトウエアを開発できる環境が整いつつある。本稿では、代表的なモデルベース設計ツールとその活用事例などを紹介した上で、組み込み用ソフト開発の現状についてまとめる。 無償の工学技術計算ツール「Mathcad Express」を使ってみた
無償の工学技術計算ツール「Mathcad Express」を使ってみた
設計計算や制御計算など高度な活用から、日常使いのローエンドな活用まで幅広い、無償の工学技術計算ツール「PTC Mathcad Express」を使ってみた。「単位をごっちゃにして数式を書いても計算してくれる」など便利機能がいろいろある。仕事での面倒くさい計算が楽しくなる、かも!?
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

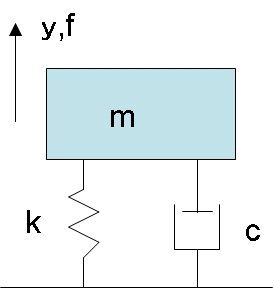 図2:振動問題
図2:振動問題
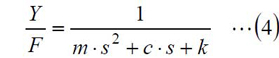

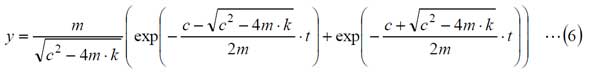
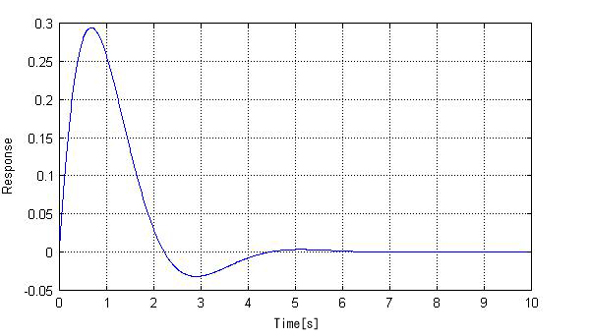 図3:インパルス応答
図3:インパルス応答






