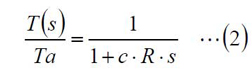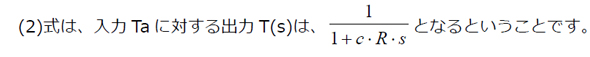伝熱問題や振動問題をラプラス変換を使って解く:無償ソフトで技術計算しよう【制御工学基礎編】(2)(1/2 ページ)
今回は、モデル化とモデル化したものの扱いを容易にする演算子法について説明する。実用に則した伝熱問題と振動問題を用いる。
対象となるものを制御工学で扱うためには、数式モデルにしなければなりません。今回は、モデル化とモデル化したものの扱いを容易にする演算子法について説明します。モデルの題材としては、実用に則した伝熱問題と振動問題を用いることにします。
伝熱問題
図1に示すように、雰囲気温度Ta[℃]の中にある物体の温度T[℃]について考えます。物体内部は一様な温度と仮定すると、ある瞬間の物体の温度変化はその物体に出入りする熱量に比例するため、下記の式が成り立ちます。
ここで、cは熱容量[J/℃]、Rは熱抵抗[℃s/J]です。
(1)式あるいは、変形した下記の(1‘)式が伝熱問題の微分方程式となります。
さて、微分方程式が代数方程式のように四則演算だけで扱えたら便利ですが、それを可能とするのが演算子法です。演算子法は、表1のように左側の関数と右側の演算子を施した結果とを機械的に対応させて、微分方程式を扱う方法です。
左側が演算子を施す前の関数で、原関数と呼ばれます。また、右側は演算子を施した後の関数で、像関数と呼ばれます。制御工学では時間変化を見るため、左側の原関数の変数は時間tとなります。一方の像関数の変数はsになります。演算子法はヘビサイドにより考案され、ラプラスにより数学的証明が与えられたため、一般には、「ラプラス変換」と呼ばれます。
表1は代表的なラプラス変換を示したものです。原関数を左側から探し出すと、該当する右側の欄が変換後の関数、すなわち像関数となります。また、像関数を四則演算により整えた後、右側の欄から探し出すと該当する左側の欄に原関数が得られます。
制御工学では、演算子を施した表1右側、すなわち像関数を使い、安定性などを評価します。
それでは、(1´)式を演算子法により解いてみます。
制御工学では、微分方程式を解かずに、(1)式に初期温度が0として演算子を施した下記の式を扱います。
右辺は伝達関数と呼ばれます。流体・伝熱などのプロセス系では、(2)式の形になることがほとんどで、「一次遅れ系」と呼ばれます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
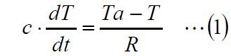

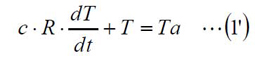
 図1:雰囲気温度Ta[℃]内の物体
図1:雰囲気温度Ta[℃]内の物体 表1:ラプラス変換表
表1:ラプラス変換表